Question

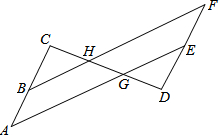已知：如图，AC∥DF，点为线段AC上一点，连接BF交DC于点H，过点作AE∥BF分别交DC、DF于点G、点，DG=CH，求证：△DFH≌△CAG．

Answer 1

考点：全等三角形的判定

专题：证明题

分析：先根据平行线的性质得出∠C=∠D，∠AGC=∠DHF，再由DG=CH可知CH+HG=HG+DG，即CG=DH，根据ASA定理即可得出结论．

解答：证明：∵AC∥DF，AE∥BF，
∴∠C=∠D，∠AGC=∠DHF，
∵DG=CH，
∴CH+HG=HG+DG，即CG=DH，
在△DFH和△CAG中，

∠C=∠D CG=DH ∠AGC=∠DHF

，
∴△DFH≌△CAG（ASA）．

点评：本题考查的是全等三角形的判定，熟知两角及其夹边分别对应相等的两个三角形全等是解答此题的关键．