题目内容
10.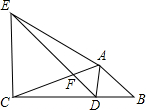 如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时.
如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时.(1)求证:△ABD是等边三角形;
(2)连接CE,若AB=2,CD=4,求CE的长.
分析 (1)根据旋转的性质得到AD=AB,∠ADE=∠B,由平行线的性质得到∠ADE=∠DAB,等量代换得到∠DAB=∠B,求得AD=BD,于是得到结论;
(2)过A作AH⊥CD于H,解直角三角形得到AH=$\sqrt{3}$,BH=1,求得DH=1,得到CH=5,根据勾股定理得到AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=$\sqrt{26}$,根据旋转的性质得到∠EAC=∠DAB=60°,AE=AC,即可得到结论.
解答 (1)证明:∵△ABC绕点A顺时针旋转一定角度得到△ADE,
∴AD=AB,
∴∠ADE=∠B,
∵DE∥AB,
∴∠ADE=∠DAB,
∴∠DAB=∠B,
∴AD=BD,
∴AD=BD=AB,
∴△ABD是等边三角形;
(2)解: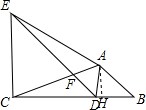 过A作AH⊥CD于H,
过A作AH⊥CD于H,
∵∠B=60°,AB=2,
∴AH=$\sqrt{3}$,BH=1,
∵BD=AB=2,
∴DH=1,
∴CH=5,
∴AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=$\sqrt{26}$,
∵△ABC绕点A顺时针旋转一定角度得到△ADE,
∴∠EAC=∠DAB=60°,AE=AC,
∴△ACE是等边三角形,
∴CE=AC=$\sqrt{26}$.
点评 本题考查了本题考查了全等三角形的性质和判定,等边三角形的判定和性质,旋转的性质,解直角三角形,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列图形中,属于数轴的是( )
| A. |  | B. |  | C. |  | D. |  |
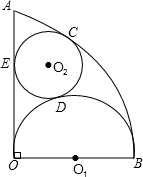 如图,扇形AOB的半径为4,∠AOB=90°,O1是以OB为直径的半圆的圆心,⊙O2与$\widehat{AB}$、半圆O1、OA分别相切于点C、D、E,求⊙O2的半径.
如图,扇形AOB的半径为4,∠AOB=90°,O1是以OB为直径的半圆的圆心,⊙O2与$\widehat{AB}$、半圆O1、OA分别相切于点C、D、E,求⊙O2的半径.
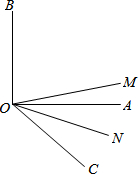 已知:如图,ON平分∠AOC,OM平分∠BOC,∠AOB=90°;
已知:如图,ON平分∠AOC,OM平分∠BOC,∠AOB=90°;