题目内容

1．一个正多边形的每个内角都等于140°，那么它是正（　　）边形．
A．正六边形B．正七边形C．正八边形D．正九边形

分析 首先根据正多边形相邻的内角与外角互补可得外角度数，再用外角和除以外角度数可得边数．

解答 解：∵正多边形的每个内角都等于140°，
∴它的每一个外角都是180°-140°=40°，
∴它的边数为：360÷40=9，
故选：D．

点评 此题主要考查了多边的内角和外角，关键是掌握多边形相邻的内角与外角互补，多边形为角和为360°．

练习册系列答案
相关题目
11．有一半圆片（其中圆心角∠AED=52°）在平面直角坐标系中，按如图所示放置，若点A可以沿y轴正半轴上下滑动，同时点B相应地在x轴正半轴上滑动，当∠OAB=n°时，半圆片上的点D与原点O距离最大，则n为（　　）°．
A．64B．52C．38D．26
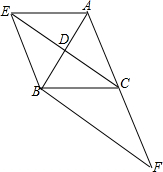12．已知，如图，在三角形ABC中，CD是中线，过点A作平行线BC的平行线，交CD的延长线于点E，连接EB．
（1）求证：四边形AEBC是平行四边形；
（2）延长AC到点F，使CF=AC，连接BF，当三角形ABF满足条件∠ABF=90°时，四边形AEBC是菱形？请证明．
9．计算：sin245°+cot60°•cos30°=1．
16．先化简，再求值：$\frac{x-3}{3{x}^{2}-6x}$÷（x+2-$\frac{5}{x-2}$），其中x满足x（x2-4）=0．
6．“我的家生活广场”用12000元购进A、B两种商品共250件，其中A种商品每件进价45元，售价60元；B种商品每件进价50元，售价70元．
（1）该百货商场购进A、B两种商品各多少件？
（2）商场第二次以原进价购进A、B两种商品，购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原售价出售，而B种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于4500元，B种商品最低售价为每件多少元？
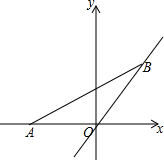13．如图，点A的坐标为（-1，0），点B（a，a），当线段AB最短时，点B的坐标为（-$\frac{1}{2}$，-$\frac{1}{2}$）．
10．用科学记数法表示0.000 000 000 000 002 56为（　　）
A．0.256×10-14B．2.56×10-15C．0.256×10-15D．256×10-17
11．阅读下列各式从左到右的变形
（1）$\frac{0.2a+b}{a+0.2b}=\frac{2a+b}{a+2b}$
（2）$-\frac{x+1}{x-y}=\frac{-x+1}{x-y}$
（3）$\frac{1}{x-y}+\frac{1}{x+y}=（x+y）+（x-y）$
（4）$\frac{{{a^2}+1}}{a}=a+1$
你认为其中变形正确的有（　　）
A．3个B．2个C．1个D．0个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网