题目内容
13.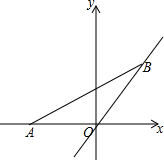 如图,点A的坐标为(-1,0),点B(a,a),当线段AB最短时,点B的坐标为(-$\frac{1}{2}$,-$\frac{1}{2}$).
如图,点A的坐标为(-1,0),点B(a,a),当线段AB最短时,点B的坐标为(-$\frac{1}{2}$,-$\frac{1}{2}$).
分析 过点A作AD⊥OB于点D,过点D作OE⊥x轴于点E,先根据垂线段最短得出当点B与点D重合时线段AB最短,再根据直线OB的解析式为y=x得出△AOD是等腰直角三角形,故OE=$\frac{1}{2}$OA=$\frac{1}{2}$,由此可得出结论.
解答  解:过点A作AD⊥OB于点D,过点D作OE⊥x轴于点E,
解:过点A作AD⊥OB于点D,过点D作OE⊥x轴于点E,
∵垂线段最短,
∴当点B与点D重合时线段AB最短.
∵直线OB的解析式为y=x,
∴△AOD是等腰直角三角形,
∴OE=$\frac{1}{2}$OA=1,
∴D(-$\frac{1}{2}$,-$\frac{1}{2}$).
故答案为:(-$\frac{1}{2}$,-$\frac{1}{2}$).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.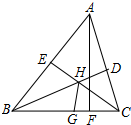 如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
 如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.一个正多边形的每个内角都等于140°,那么它是正( )边形.
| A. | 正六边形 | B. | 正七边形 | C. | 正八边形 | D. | 正九边形 |
8.下列说法中正确的个数是( )
①一个数与它的相反数的商为-1;
②两个有理数之和大于其中任意一个加数;
③若两数之和为正数,则这两个数一定都是正数;
④若m<0<n,则mn<n-m.
①一个数与它的相反数的商为-1;
②两个有理数之和大于其中任意一个加数;
③若两数之和为正数,则这两个数一定都是正数;
④若m<0<n,则mn<n-m.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
2.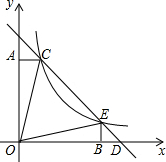 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )| A. | ①②③ | B. | ①②③④ | C. | ②③④⑤ | D. | ①②⑤ |
3.如果两条直线被第三条直线所截,那么一组内错角的平分线( )
| A. | 互相垂直 | B. | 互相平行 | C. | 互相重合 | D. | 不能确定 |