题目内容
16.先化简,再求值:$\frac{x-3}{3{x}^{2}-6x}$÷(x+2-$\frac{5}{x-2}$),其中x满足x(x2-4)=0.分析 先把括号内通分和把除法运算化为乘法运算,再把分子分母因式分解,约分得到原式$\frac{1}{3{x}^{2}+9x}$,接着解x(x2-4)=0,然后利用分式有意义的条件确定x的值,再把x的值代入计算即可.
解答 解:原式=$\frac{x-3}{3x(x-2)}$÷$\frac{(x+2)(x-2)-5}{x-2}$
=$\frac{x-3}{3x(x-2)}$•$\frac{x-2}{(x+3)(x-3)}$
=$\frac{1}{3x(x+3)}$
=$\frac{1}{3{x}^{2}+9x}$,
解x(x2-4)=0得x=0或x=2或x=-2,
因为x≠0且x≠2,
所以x=-2,
当x=-2时,原式=$\frac{1}{3×(-2)^{2}+9×(-2)}$=-$\frac{1}{6}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
7.不解方程,判断方程2x2-4x-1=0的根的情况( )
| A. | 没有实数根 | B. | 有两个相等实数根 | ||
| C. | 有两个不相等实数根 | D. | 无法确定 |
1.一个正多边形的每个内角都等于140°,那么它是正( )边形.
| A. | 正六边形 | B. | 正七边形 | C. | 正八边形 | D. | 正九边形 |
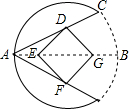 如图,在圆的正中央摆放着一个正方形DEFG,且正方形的顶点D在弦AC上、对角线EG在直径AB上.若EG=4,AB=8,则AC=$\frac{16\sqrt{5}}{5}$.
如图,在圆的正中央摆放着一个正方形DEFG,且正方形的顶点D在弦AC上、对角线EG在直径AB上.若EG=4,AB=8,则AC=$\frac{16\sqrt{5}}{5}$.