题目内容
12. 如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=$\frac{1}{2}$S△BCD,求点P的坐标.
分析 (1)设抛物线顶点式解析式y=a(x-1)2+4,然后把点B的坐标代入求出a的值,即可得解;
(2)令y=0,解方程得出点C,D坐标,再用三角形面积公式即可得出结论;
(3)先根据面积关系求出点P的坐标,求出点P的纵坐标,代入抛物线解析式即可求出点P的坐标.
解答 解:(1)∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x-1)2+4,
把点B(0,3)代入得,a+4=3,
解得a=-1,
∴抛物线的解析式为y=-(x-1)2+4;
(2)由(1)知,抛物线的解析式为y=-(x-1)2+4;
令y=0,则0=-(x-1)2+4,
∴x=-1或x=3,
∴C(-1,0),D(3,0);
∴CD=4,
∴S△BCD=$\frac{1}{2}$CD×|yB|=$\frac{1}{2}$×4×3=6;
(3)由(2)知,S△BCD=$\frac{1}{2}$CD×|yB|=$\frac{1}{2}$×4×3=6;CD=4,
∵S△PCD=$\frac{1}{2}$S△BCD,
∴S△PCD=$\frac{1}{2}$CD×|yP|=$\frac{1}{2}$×4×|yP|=3,
∴|yP|=$\frac{3}{2}$,
∵点P在x轴上方的抛物线上,
∴yP>0,
∴yP=$\frac{3}{2}$,
∵抛物线的解析式为y=-(x-1)2+4;
∴$\frac{3}{2}$=-(x-1)2+4,
∴x=1±$\frac{\sqrt{10}}{2}$,
∴P(1+$\frac{\sqrt{10}}{2}$,$\frac{3}{2}$),或P(1-$\frac{\sqrt{10}}{2}$,$\frac{3}{2}$).
点评 此题是二次函数综合题,主要考查了待定系数法,坐标轴上点的特点,三角形的面积公式,解本题的关键是求出抛物线解析式,是一道比较简单的中考常考题.

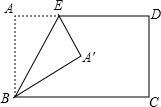 如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
| A. | $\sqrt{2}-\sqrt{3}$ | B. | 2$-\sqrt{3}$ | C. | 3$\sqrt{2}$-2$\sqrt{3}$ | D. | $\sqrt{2}$ |
| A. | tan50°-sin50° | B. | sin50°-tan50° | C. | 2-sin50°-tan50° | D. | -sin50°-tan50° |
| A. | 2或12 | B. | -2或-12 | C. | 2或-12 | D. | -2或12 |
| A. | 2x+3y=5xy | B. | 5m2•m3=5m5 | C. | a6÷a3=a2 | D. | (m2)3=m5 |