题目内容
12.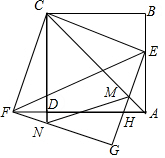 如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.
如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.(1)证明:点A、D、F在同一条直线上;
(2)随着点E的移动,线段DH是否有最小值?若有,求出最小值;若没有,请说明理由;
(3)连结EF、MN,当MN∥EF时,求AE的长.
分析 (1)由△DCF≌△BCE,可得∠CDF=∠B=90°,即可推出∠CDF+∠CDA=180°,由此即可证明.
(2)有最小值.设AE=x,DH=y,则AH=1-y,BE=1-x,由△ECB∽△HEA,推出$\frac{BC}{AE}$=$\frac{BE}{AH}$,可得$\frac{1}{x}$=$\frac{1-x}{1-y}$,推出y=x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$,由a=1>0,y有最小值,最小值为$\frac{3}{4}$.
(3)只要证明△CFN≌△CEM,推出∠FCN=∠ECM,由∠MCN=45°,可得∠FCN=∠ECM=∠BCE=22.5°,在BC上取一点G,使得GC=GE,则△BGE是等腰直角三角形,设BE=BG=a,则GC=GE=$\sqrt{2}$a,可得a+$\sqrt{2}$a=1,求出a即可解决问题;
解答 (1)证明:∵四边形ABCD是正方形,
∴CD=CB,∠BCD=∠B=∠ADC=90°,
∵CE=CF,∠ECF=90°,
∴∠ECF=∠DCB,
∴∠DCF=∠BCE,
∴△DCF≌△BCE,
∴∠CDF=∠B=90°,
∴∠CDF+∠CDA=180°,
∴点A、D、F在同一条直线上.
(2)解:有最小值.
理由:设AE=x,DH=y,则AH=1-y,BE=1-x,
∵四边形CFGE是矩形,
∴∠CEG=90°,
∴∠CEB+∠AEH=90°
CEB+∠ECB=90°,
∴∠ECB=∠AEH,
∵∠B=∠EAH=90°,
∴△ECB∽△HEA,
∴$\frac{BC}{AE}$=$\frac{BE}{AH}$,
∴$\frac{1}{x}$=$\frac{1-x}{1-y}$,
∴y=x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$,
∵a=1>0,
∴y有最小值,最小值为$\frac{3}{4}$.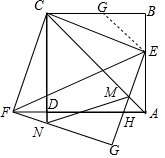
∴DH的最小值为$\frac{3}{4}$.
(3)解:∵四边形CFGE是矩形,CF=CE,
∴四边形CFGE是正方形,
∴GF=GE,∠GFE=∠GEF=45°,
∵NM∥EF,
∴∠GNM=∠GFE,∠GMN=∠GEF,
∴∠GMN=∠GNM,
∴GN=GM,
∴FN=EM,
∵CF=CE,∠CFN=∠CEM,
∴△CFN≌△CEM,
∴∠FCN=∠ECM,∵∠MCN=45°,
∴∠FCN=∠ECM=∠BCE=22.5°,
在BC上取一点G,使得GC=GE,则△BGE是等腰直角三角形,设BE=BG=a,则GC=GE=$\sqrt{2}$a,
∴a+$\sqrt{2}$a=1,
∴a=$\sqrt{2}$-1,
∴AE=AB-BE=1-($\sqrt{2}$-1)=2-$\sqrt{2}$.
点评 本题考查四边形综合题、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用所学知识解决问题,学会构建二次函数解决最值问题,学会用方程的思想思考问题,属于中考压轴题.


| A. | 全 | B. | 明 | C. | 城 | D. | 市 |
| A. | m=$\frac{5}{3}$ | B. | m=3 | C. | m=$\frac{5}{3}$或1 | D. | m=$\frac{5}{3}$或3 |
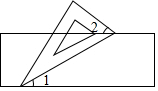 如图,小聪把一块含有60°角的直角三角形板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是( )
如图,小聪把一块含有60°角的直角三角形板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 60° |
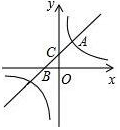 如图,直线y=x+b与双曲线y=$\frac{k}{x}$(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
如图,直线y=x+b与双曲线y=$\frac{k}{x}$(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点. 如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.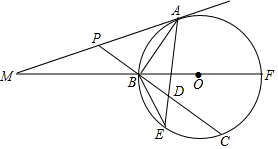 如图,已知BF是⊙O的直径,A为⊙O上(异于B、F)一点,⊙O的切线MA与FB的延长线交于点M;P为AM上一点,PB的延长线交⊙O于点C,D为BC上一点且PA=PD,AD的延长线交⊙O于点E.
如图,已知BF是⊙O的直径,A为⊙O上(异于B、F)一点,⊙O的切线MA与FB的延长线交于点M;P为AM上一点,PB的延长线交⊙O于点C,D为BC上一点且PA=PD,AD的延长线交⊙O于点E.