题目内容
17.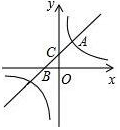 如图,直线y=x+b与双曲线y=$\frac{k}{x}$(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
如图,直线y=x+b与双曲线y=$\frac{k}{x}$(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
分析 (1)把A(1,2)代入双曲线以及直线y=x+b,分别可得k,b的值;
(2)先根据直线解析式得到BO=CO=1,再根据△BCP的面积等于2,即可得到P的坐标.
解答 解:(1)把A(1,2)代入双曲线y=$\frac{k}{x}$,可得k=2,
∴双曲线的解析式为y=$\frac{2}{x}$;
把A(1,2)代入直线y=x+b,可得b=1,
∴直线的解析式为y=x+1;
(2)设P点的坐标为(x,0),
在y=x+1中,令y=0,则x=-1;令x=0,则y=1,
∴B(-1,0),C(0,1),即BO=1=CO,
∵△BCP的面积等于2,
∴$\frac{1}{2}$BP×CO=2,即$\frac{1}{2}$|x-(-1)|×1=2,
解得x=3或-5,
∴P点的坐标为(3,0)或(-5,0).
点评 本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与一次函数交点的坐标同时满足两个函数解析式.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
8.先化简,再求值($\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{2-x}{x-2}$)÷$\frac{x}{x-2}$(其中x=3),其计算结果是( )
| A. | -$\frac{4}{3}$ | B. | 4 | C. | -4 | D. | $\frac{4}{3}$ |
2. 如图是一个几何体的三视图,则这个几何体是( )
如图是一个几何体的三视图,则这个几何体是( )
 如图是一个几何体的三视图,则这个几何体是( )
如图是一个几何体的三视图,则这个几何体是( )| A. |  | B. |  | C. |  | D. |  |
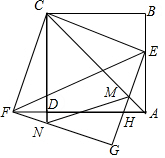 如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.
如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.