题目内容
4. 如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
分析 (1)由BE∥CO,推出∠OCB=∠CBE,由OC=OB,推出∠OCB=∠OBC,可得∠CBE=∠CBO;
(2)在Rt△CDO中,求出OD,由OC∥BE,可得$\frac{DC}{CE}$=$\frac{DO}{OB}$,由此即可解决问题;
解答 (1)证明: ∵DE是切线,
∵DE是切线,
∴OC⊥DE,
∵BE∥CO,
∴∠OCB=∠CBE,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBE=∠CBO,
∴BC平分∠ABE.
(2)在Rt△CDO中,∵DC=8,OC=0A=6,
∴OD=$\sqrt{C{D}^{2}+O{C}^{2}}$=10,
∵OC∥BE,
∴$\frac{DC}{CE}$=$\frac{DO}{OB}$,
∴$\frac{8}{CE}$=$\frac{10}{6}$,
∴EC=4.8.
点评 本题考查切线的性质、平行线的性质、角平分线的定义、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
13.下表是某位男子马拉松长跑运动员近6次的比赛成绩(单位:分钟)
则这组成绩的中位数和平均数分别为( )
| 第几次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 比赛成绩 | 145 | 147 | 140 | 129 | 136 | 125 |
| A. | 137、138 | B. | 138、137 | C. | 138、138 | D. | 137、139 |
14.下列计算正确的是( )
| A. | b3•b3=2b3 | B. | (a+2)(a-2)=a2-4 | ||
| C. | (ab2)3=ab6 | D. | (8a-7b)-(4a-5b)=4a-12b |
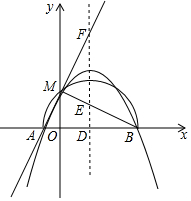 已知二次函数y=-x2+bx+c+1,
已知二次函数y=-x2+bx+c+1,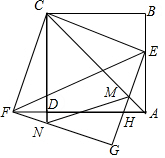 如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.
如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.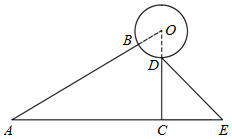 某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.
某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.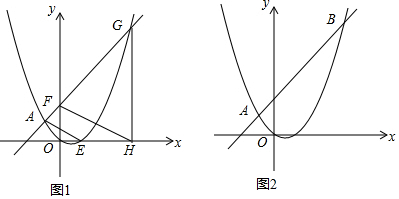
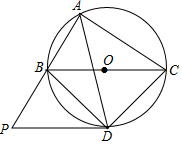 如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.