题目内容
20.若关于x的方程$\frac{3-2x}{x-3}$-$\frac{mx-2}{3-x}$=-1无解,则m的值是( )| A. | m=$\frac{5}{3}$ | B. | m=3 | C. | m=$\frac{5}{3}$或1 | D. | m=$\frac{5}{3}$或3 |
分析 分式方程去分母转化为整式方程,由分式方程无解确定出x的值,代入整式方程计算即可求出m的值.
解答 解:去分母得:3-2x+mx-2=-x+3,
整理得:(m-1)x=2,
当m-1=0,即m=1时,方程无解;
当m-1≠1时,x-3=0,即x=3时,方程无解,此时$\frac{2}{m-1}$=3,即m=$\frac{5}{3}$,
故选C
点评 此题考查了分式方程的解,分式方程无解分为最简公分母为0的情况与分式方程转化为的整式方程无解的情况.

练习册系列答案
相关题目
11.下面的图形中,是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.先化简,再求值($\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{2-x}{x-2}$)÷$\frac{x}{x-2}$(其中x=3),其计算结果是( )
| A. | -$\frac{4}{3}$ | B. | 4 | C. | -4 | D. | $\frac{4}{3}$ |
10.化简$\frac{4x}{{x}^{2}-4}$-$\frac{x}{x-2}$的结果是( )
| A. | -x2+2x | B. | -x2+6x | C. | -$\frac{x}{x+2}$ | D. | $\frac{x}{x-2}$ |
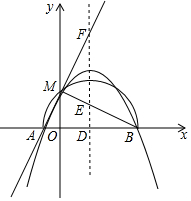 已知二次函数y=-x2+bx+c+1,
已知二次函数y=-x2+bx+c+1,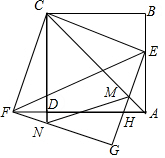 如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.
如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.