题目内容
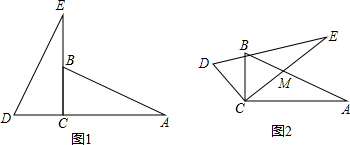
 如图,在△ABC中,若BD:DC=CE:EA=2:1,AD和BE交于F,求AF:FD.
如图,在△ABC中,若BD:DC=CE:EA=2:1,AD和BE交于F,求AF:FD.考点:平行线分线段成比例
专题:
分析:如图,作辅助线,首先证明BD:DC=EG:GC=2:1;设GC=λ,则EG=2λ,EC=3λ;证明AE=
,根据平行线分线段成比例定理,列出比例式即可解决问题.
| 3λ |
| 2 |
解答: 解:如图,过点D作DG∥BE,交AC于点G.
解:如图,过点D作DG∥BE,交AC于点G.
则BD:DC=EG:GC=2:1,
设GC=λ,则EG=2λ,EC=3λ;
∵EC:AE=2:1,
∴AE=
×3λ=
;
∵EF∥DG,
∴AF:FD=AE:EG=
:2λ,
∴AF:FD=3:4.
 解:如图,过点D作DG∥BE,交AC于点G.
解:如图,过点D作DG∥BE,交AC于点G.则BD:DC=EG:GC=2:1,
设GC=λ,则EG=2λ,EC=3λ;
∵EC:AE=2:1,
∴AE=
| 1 |
| 2 |
| 3λ |
| 2 |
∵EF∥DG,
∴AF:FD=AE:EG=
| 3λ |
| 2 |
∴AF:FD=3:4.
点评:该题主要考查了平行线分线段成比例定理及其应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 画出下图中的五块小立方块的搭法的三视图.
画出下图中的五块小立方块的搭法的三视图.
 如图,抛物线y=-x2+2x的顶点为M,点P为第四象限的抛物线上一点,以PM为直径的⊙O′恰好以过点O,求P点的坐标.
如图,抛物线y=-x2+2x的顶点为M,点P为第四象限的抛物线上一点,以PM为直径的⊙O′恰好以过点O,求P点的坐标. 如图,∠AOB=37°,∠AOC=24°,∠BOC=
如图,∠AOB=37°,∠AOC=24°,∠BOC=