题目内容
17.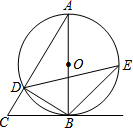 如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.(1)求证:BC为⊙O的切线;
(2)若E为$\widehat{AB}$中点,BD=6,$sin∠BED=\frac{3}{5}$,求BE的长.
分析 (1)由圆周角定理和已知条件证出∠CBD+∠ABD=90°.得出∠ABC=90°,即可得出结论.
(2)连接AE.由圆周角定理得出∠BAD=∠BED,得出$sin∠BAD=\frac{BD}{AB}=\frac{3}{5}$.求出直径AB=10.证出AE=BE.得出△AEB是等腰直角三角形.得出∠BAE=45°,由三角函数即可得出结果.
解答 (1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠A+∠ABD=90°.
又∵∠A=∠CBD,
∴∠CBD+∠ABD=90°.
∴∠ABC=90°.
∴AB⊥BC.
又∵AB是⊙O的直径,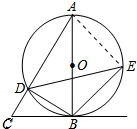
∴BC为⊙O的切线.
(2)解:连接AE.如图所示:
∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°.
∵∠BAD=∠BED,
∴$sin∠BAD=sin∠BED=\frac{3}{5}$.
∴在Rt△ABD中,$sin∠BAD=\frac{BD}{AB}=\frac{3}{5}$.
∵BD=6,
∴AB=10.
∵E为$\widehat{AB}$ 中点,
∴AE=BE.
∴△AEB是等腰直角三角形.
∴∠BAE=45°.
∴$BE=AB•sin∠BAE=10×\frac{{\sqrt{2}}}{2}=5\sqrt{2}$.
点评 本题考查了切线的判定定理、圆周角定理、三角函数、等腰直角三角形的判定与性质等知识;熟练掌握切线的判定,由三角函数求出直径是解决问题(2)的关键.

练习册系列答案
相关题目
5.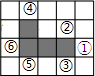 如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
 如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,小亮将边长为3的正方形铁丝框ABCD变形为正六边形为EFMNPQ(忽略铁丝的粗细),则所得正六边形的面积为6$\sqrt{3}$.
如图,小亮将边长为3的正方形铁丝框ABCD变形为正六边形为EFMNPQ(忽略铁丝的粗细),则所得正六边形的面积为6$\sqrt{3}$.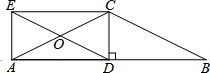 如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.
如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.
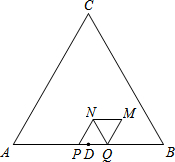 如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).
如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3). 如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C.
如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C. 如图,△ABC中,AB=AC,以边BC为直径的⊙O与边AB,AC分别交于D,F两点,过点D作⊙O的切线DE,使DE⊥AC于E.
如图,△ABC中,AB=AC,以边BC为直径的⊙O与边AB,AC分别交于D,F两点,过点D作⊙O的切线DE,使DE⊥AC于E.