题目内容
6. 如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C.
如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C.(1)求证:AB是⊙O的切线;
(2)若AB=4cm,AD=2cm,求tanA的值和DB的长.
分析 (1)连结OB,由等腰三角形的性质和圆周角定理证出∠CDB+∠C=90°,再由已知条件得出∠OBD+∠ABD=90°,得出∠OBA=90°即可;
(2)设半径为r,则OA=x+2,在Rt△AOB中,根据勾股定理得出方程,解方程求出半径,由三角函数求出得出tanA=$\frac{OB}{AB}$=$\frac{3}{4}$,证明△ADB∽△ACB,得出$\frac{DB}{BC}=\frac{AD}{AB}$=$\frac{1}{2}$,设DB=x,则BC=2x,由勾股定理得出方程,解方程即可.
解答 (1)证明:连结OB,如图所示: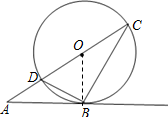
∵OB=OD,
∴∠ODB=∠OBD,
∵DC是⊙O的直径,
∴∠DBC=90°,
∴∠CDB+∠C=90°,
∵∠ABD=∠C,
∴∠OBD+∠ABD=90°,
即∠OBA=90°,
∴OB⊥AB,
∴AB是⊙O的切线;
(2)解:设半径为r,则OA=x+2,
在Rt△AOB中,根据勾股定理得:x2+42=(x+2)2,
解得:r=3,
∴tanA=$\frac{OB}{AB}$=$\frac{3}{4}$,
∵∠A=∠A,∠ABD=∠C,
∴△ADB∽△ACB,
∴$\frac{DB}{BC}=\frac{AD}{AB}$=$\frac{2}{4}$=$\frac{1}{2}$,
设DB=x,则BC=2x,
∵CD=6,
∴由勾股定理得:x2+(2x)2=62,
解得:x=$\frac{6}{5}$$\sqrt{5}$,
即DB的长为$\frac{6}{5}$$\sqrt{5}$.
点评 本题考查了切线的判定、圆周角定理、等腰三角形的性质、勾股定理、三角函数、相似三角形的判定与性质;熟练掌握切线的判定方法,由勾股定理求出半径是解决问题(2)的关键.

练习册系列答案
相关题目
15.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
下列说法正确的是( )
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
| A. | 抛物线的开口向下 | B. | 当x>-3时,y随x的增大而增大 | ||
| C. | 二次函数的最小值是-2 | D. | 抛物线的对称轴是x=-$\frac{5}{2}$ |
16.下列各图中,∠1与∠2互为余角的是( )
| A. |  | B. |  | C. |  | D. |  |
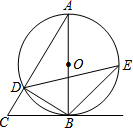 如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.