题目内容
7．
如图，小亮将边长为3的正方形铁丝框ABCD变形为正六边形为EFMNPQ（忽略铁丝的粗细），则所得正六边形的面积为6$\sqrt{3}$．
分析 先求出铁丝的长，再求出正六边形的边长，连接OQ，OP，进而可得出结论．
解答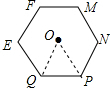 
解：∵正方形铁丝框ABCD的边长为3，
∴铁丝长=3×4=12，
∴正六边形为EFMNPQ的边长=$\frac{12}{6}$=2．
连接OQ，OP，
∵∠OQP=∠OPQ=60°，
∴△OPQ是正三角形，
∴S正六边形为EFMNPQ=6S△OQP=6×$\frac{1}{2}$×2×2sin60°=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$．
故答案为：6$\sqrt{3}$．
点评 本题考查的是正多边形和圆，根据题意作出辅助线，构造出等边三角形是解答此题的关键．
练习册系列答案
相关题目
如图，AE是正八边形ABCDEFGH的一条对角线，则∠BAE=67.5°．
在△ABC中，∠BAC=90°，BC的垂直平分线EF交BC于点F，交AB于点E，P是AC延长线上一点，连接FP，将FP绕点F逆时针旋转2α，得到FK，如果∠B=α（0°＜α＜90°），则$\frac{CK-CP}{cosα•EF}$=2．
19．
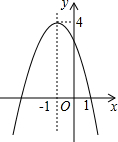如图是二次函数：y=ax2+bx+c（a≠0）的图象，下列说法错误的是（ ）
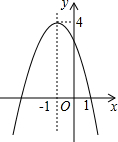如图是二次函数：y=ax2+bx+c（a≠0）的图象，下列说法错误的是（ ）| A． | 函数y的最大值是4 | B． | 函效的图象关于直线x=-1对称 | ||
| C． | 当x＜-1时，y随x的增大而增大 | D． | 当-4＜x＜1时，函数值y＞0 |
如图，已知△ABC，以AB为直径的⊙O交AC于点D，∠CBD=∠A．