题目内容
19.从长度分别为3cm,4cm,6cm,8cm,10cm的五条线段中任取三条,若每条线段被取到的可能性相同,则取到的三条线段可以组成三角形的概率是( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{7}{10}$ |
分析 首先写出所有的组合情况,再根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,分析得到能够组成三角形的情况,从而求得概率.
解答 解:其中的任意三条组合共有3,10,8; 3,10,6; 3,10,4; 3,8,6; 3,8,4; 3,6,4; 10,8,6; 10,8,4; 10,6,4; 8,6,4十种情况.
根据三角形的三边关系,知其中的3,8,4; 3,8,6; 3,4,6; 6、8、10; 10、8、4;8、6、4能组成三角形,
∴取到的三条线段可以组成三角形的概率是$\frac{6}{10}$=$\frac{3}{5}$,
故选:A.
点评 此题综合考查了从三角形的三边关系和概率的计算方法.用到的知识点为:概率=所求情况数与总情况数之比;三角形的两个较小的边的和大于最大的边的边长.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
10.下列运算正确的是( )
| A. | $\sqrt{(-3)^{2}}$=3 | B. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ | D. | $\sqrt{5}$-$\sqrt{2}$=$\sqrt{3}$ |
14.下列计算中,正确的是( )
| A. | (-3a2b)3=27a6b3 | B. | (a4)3=a7 | C. | a12÷a4=a8 | D. | a2•a4=a8 |
4.抛物线y=-3(x+1)2+3的顶点坐标是( )
| A. | (-1,3) | B. | (1,3) | C. | (-1,-3) | D. | (0,3) |
11.下列计算结果中,正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{(-4)(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$=6 | C. | $\sqrt{12}$$-\sqrt{3}$=$\sqrt{3}$ | D. | $\sqrt{(-7)^{2}}$=±7 |
8.若关于x的方程x2+5x+a=0有一个根为-2,则a的值是( )
| A. | 6 | B. | -6 | C. | 14 | D. | -14 |
9.下列成语所描述的事件为必然事件的是( )
| A. | 水中捞月 | B. | 瓮中捉鳖 | C. | 守株待兔 | D. | 拔苗助长 |
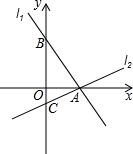 如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.
如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.