题目内容
17. 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )| A. | $\widehat{BC}$=$\frac{1}{2}$$\widehat{AC}$ | B. | $\widehat{BC}$=$\frac{1}{3}$$\widehat{AC}$ | C. | $\widehat{BC}$=$\widehat{AC}$ | D. | 不能确定 |
分析 连接OC,BC,过O作OE⊥AC于D交圆O于E,根据折叠的性质得到OD=$\frac{1}{2}$OE,根据圆周角定理得到∠ACB=90°,根据三角形的中位线的性质得到OD=$\frac{1}{2}$BC,求得∠COB=60°,得到∠AOC=120°,于是得到结论.
解答 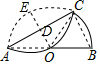 解:连接OC,BC,过O作OE⊥AC于D交圆O于E,
解:连接OC,BC,过O作OE⊥AC于D交圆O于E,
∵把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,
∴OD=$\frac{1}{2}$OE,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴OD∥BC,
∵OA=OB,
∴OD=$\frac{1}{2}$BC,
∴BC=OE=OB=OC,
∴∠COB=60°,
∴∠AOC=120°,
∴$\widehat{BC}$=$\frac{1}{2}$$\widehat{AC}$,
故选A.
点评 本题考查了圆心角,弧,弦的关系,垂径定理,三角形的中位线的性质,折叠的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
5.一个不透明的盒子中装有3个红球,2个黄球和1个白球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
6.下列各数是无理数的是( )
| A. | 3.1415926 | B. | $\root{3}{8}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | $\sqrt{\frac{64}{121}}$ |
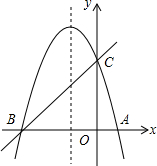 如图,已知抛物线y=-x2+bx+c的对称轴为直线x=-1,与y轴交于点C(0,3),与x轴交于点A和点B.
如图,已知抛物线y=-x2+bx+c的对称轴为直线x=-1,与y轴交于点C(0,3),与x轴交于点A和点B. 如图,平面直角坐标系中,点A是直线y=$\frac{b}{a}x$(a≠0)上一点,过点A作AB⊥x轴于点B(2,0),若点C(4-a,b),且AC⊥OC,∠AOC=45°,OC与AB交于点D,求AD的长.
如图,平面直角坐标系中,点A是直线y=$\frac{b}{a}x$(a≠0)上一点,过点A作AB⊥x轴于点B(2,0),若点C(4-a,b),且AC⊥OC,∠AOC=45°,OC与AB交于点D,求AD的长.

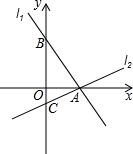 如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.
如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.