题目内容
12．已知4x2+9y2-4x-6y+2=0，求$\frac{\sqrt{y}}{\sqrt{x}+\sqrt{y}}$-$\frac{\sqrt{y}}{\sqrt{x}-\sqrt{y}}$的值．分析 先利用完全平方公式4x2+9y2-4x-6y+2=0转化为（2x-1）2+（3y-1）2=0，利用非负数的性质求出x、y，再通分化简即可．
解答 解：∵4x2+9y2-4x-6y+2=0，
∴（2x-1）2+（3y-1）2=0，
∵（2x-1）2≥0，（3y-1）2≥0，
∴x=$\frac{1}{2}$，y=$\frac{1}{3}$，
∴原式=$\frac{\sqrt{y}（\sqrt{x}-\sqrt{y}）-\sqrt{y}（\sqrt{x}+\sqrt{y}）}{（\sqrt{x}+\sqrt{y}）（\sqrt{x}-\sqrt{y}）}$=$\frac{-2y}{x-y}$=$\frac{-2×\frac{1}{3}}{\frac{1}{2}-\frac{1}{3}}$=-4．
点评 本题考查二次根式的化简求值、非负数的性质等知识，解题的关键是非负数性质的应用，掌握乘法公式，属于中考常考题型．
练习册系列答案
相关题目
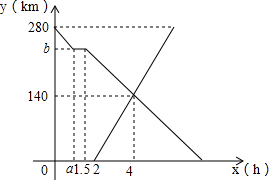甲、乙两车分别从A、B两地沿着一条笔直的公路行驶，甲车从A地开往B地，2h后乙车从B地开往A地，两车均以各自的速度匀速行驶，甲车在行驶途中出观故障，停车维修0.5h后又以原速继续匀速行驶到B地，如图是甲、乙两车与B地的距离y（km）与甲车离开A地时间x（h）之间的函数图象，根据图象解答下列问题：
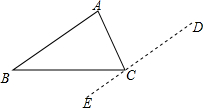请根据图给出的图示（过点C作ED∥AB），对“三角形内角和等于180°”说理．（作平行线是把角从一个位置“转移”到另一个位置的重要手段）