题目内容
如图，直线AB、CD被直线EF所截，∠1、∠2是同位角，如果∠1≠∠2，那么AB与CD不平行．用反证法证明这个命题时，应先假设：_____.
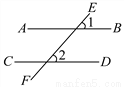
AB∥CD
【解析】试题分析：利用假设法来进行证明时，首先假设结论成立，即应先假设AB∥CD．
名校课堂系列答案已知抛物线y= -x2+mx+（7-2m）（m为常数）．
（1）证明：不论m为何值，抛物线与x轴恒有两个不同的交点；
（2）若抛物线与x轴的交点A（x1，0）、B（x2，0）的距离为AB=4（A在B的左边），且抛物线交y轴的正半轴于C，求抛物线的解析式．
（1）证明见解析；（2）抛物线的解析式为y= -x2+2x+3．
【解析】试题分析：（1）要证明抛物线与x轴恒有两个不同的交点证明抛物线的判别式是正数，所以证明判别式是正数即可解决问题；
（2）首先由AB=4可以得|x2-x1|=4，而（x2-x1）2=（x2-x1）2-4x1x2=16，然后利用根与系数的关系即可得到关于m方程，解方程即可求出m，也就求出了抛物线的解析式．
试题... 如图，长方形ABCD中，AB=2，点E在BC上并且AE=EC，若将矩形纸片沿AE折叠，使点B恰好落在AC上，则AC的长为多少？
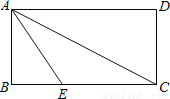
4
【解析】试题分析：根据折叠的性质及等边对等角的性质，可得到∠BAE=∠EAC=∠ECA，根据三角形内角和定理即可求得∠ECA的度数，再根据直角三角形的性质不难求得AC的长．
试题解析：如图，设点B落在AC上后，为点F.
则有△AFE≌△ABE，
∴∠AFE =∠B =90° ，AF =AB =2，
∴FE⊥AC，
∵AE=EC，
∴CF =AF =2，... 下列字母中：H、F、A、O、M、W、Y、E，轴对称图形的个数是（ ）
A. 5 B. 4 C. 6 D. 7
D
【解析】从第一个字母研究，只要能够找到一条对称轴，令这个字母沿这条对称轴折叠后，两边的部分能够互相重合，就是轴对称图形，可以得出：字母H、A、O、M、W、Y、E这七个字母，属于轴对称图形.
故选：D. 等腰三角形是轴对称图形，它的对称轴是( )
A. 过顶点的直线 B. 底边上的高
C. 顶角的平分线所在的直线 D. 腰上的高所在的直线
C
【解析】等腰三角形的对称轴为顶角平分线所在的直线，
故选C． 某地震救援队探测出某建筑物废墟下方点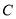
处有生命迹象,已知废墟一侧地面上两探测点A，B相距3米,探测线与地面的夹角分别是
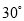和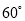
(如图),试确定生命所在点C的深度.(结果精确到
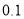米,参考数据: 
,
)
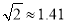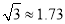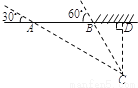
生命所在点的深度约为米
【解析】试题分析：过点C作CD⊥AB于点D，根据题意得出∠CAD=30°，∠CBD=60°，分别根据Rt△ACD和Rt△BCD的三角函数将AD和BD用含CD的代数式表示，然后根据AB=3得出答案．
试题解析：过作于点
∵探测线与地面的夹角为和， ∴,，
在Rt中, ， ∴，
在Rt中, ， ∴，
又∵ ∴ 解得，
∴生命所在点的深度... 某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y= -2x+100．（利润=售价-制造成本）
（1）写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
（1）z= -2x2+136x-1800；（2）当销售单价为34元时，每月能获得最大利润，最大利润是512万元；
【解析】试题分析：（1）根据每月的利润z=（x-18）y，再把y=-2x+100代入即可求出z与x之间的函数解析式，
（2）把z=350代入z=-2x2+136x-1800，解这个方程即可，将z═-2x2+136x-1800配方，得z=-2（x-34）2+512，即可求出当... 如图，已知抛物线y＝
x2－
x－3与x轴的交点为A、D(A在D的右侧)，与y轴的交点为C.
(1)直接写出A、D、C三点的坐标；
(2)若点M在抛物线上，使得△MAD的面积与△CAD的面积相等，求点M的坐标；
(3)设点C关于抛物线对称轴的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，请求出点P的坐标；若不存在，请说明理由．
（1）A点坐标为(4，0)，D点坐标为(－2，0)，C点坐标为(0，－3)；
（2）M点坐标为(2，－3)或(1＋，3)或(1－，3)；
（3）在抛物线上存在一点P，使得以点A、B、C、P四点为顶点所构成的四边形为梯形；点P的坐标为(－2，0)或(6，6)．
【解析】试题分析：（1）在中令，解得，
∴A(4，0) 、D(－2，0).
在中令，得，∴C(0，－3).
...