题目内容
某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y= -2x+100．（利润=售价-制造成本）
（1）写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
（1）z= -2x2+136x-1800；（2）当销售单价为34元时，每月能获得最大利润，最大利润是512万元；
【解析】试题分析：（1）根据每月的利润z=（x-18）y，再把y=-2x+100代入即可求出z与x之间的函数解析式，
（2）把z=350代入z=-2x2+136x-1800，解这个方程即可，将z═-2x2+136x-1800配方，得z=-2（x-34）2+512，即可求出当...
阅读快车系列答案若|a﹣2|+b2﹣2b+1=0，则a=__，b=__．
2 1
【解析】∵|a﹣2|+b2﹣2b+1=0，
∴|a﹣2|+(b-1)2=0，
∴a-2=0,b-1=0,
∴a=2,b=1. 如图，直线AB、CD被直线EF所截，∠1、∠2是同位角，如果∠1≠∠2，那么AB与CD不平行．用反证法证明这个命题时，应先假设：_____.
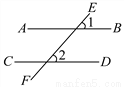
AB∥CD
【解析】试题分析：利用假设法来进行证明时，首先假设结论成立，即应先假设AB∥CD． 如图，在活动课上，小明和小红合作用一副三角板来测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是1.7m，他调整自己的位置，设法使得三角板的一条直角边保持水平，且斜边与旗杆顶端M在同一条直线上，测得旗杆顶端M仰角为45°；小红的眼睛与地面的距离（CD）是1.5m，用同样的方法测得旗杆顶端M的仰角为30°．两人相距28米且位于旗杆两侧（点B、N、D在同一条直线上）．求出旗杆MN的高度．（参考数据：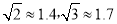 
，结果保留整数．）
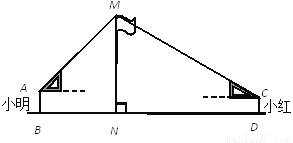
旗杆高约为12米．
【解析】试题分析：过点A作AE⊥MN于E，过点C作CF⊥MN于F，则EF=0.2m．由△AEM是等腰直角三角形得出AE=ME，设AE=ME=xm，则MF=(x+0.2)m，FC=(28-x)m．在Rt△MFC中，由MF=CF•tan∠MCF，解方程求出x的值，则MN=ME+EN．
试题解析： 过点A作AE⊥MN于E，
过点C作CF⊥MN于F
则EF= =... 如图，小敏同学想测量一棵大树的高度，她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°.已知小敏同学身高(AB)为1.6m，则这棵树的高度为(结果精确到0.1m，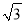 
≈1.73)( )
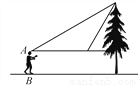
A. 3.5m B. 3.6m C. 4.3m D. 5.1m
D
【解析】如图，设CD＝xm，在Rt△ACD中，∵∠DAC＝30°，∴（m）．在Rt△ECD中，∵∠DEC＝60°，∴（m）．∵AE＝4m，∴，解得．
∴（m）．故选D． 如图，在相距2米的两棵树间拴一根绳子做一个简易的秋千.拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小芳距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为 米.
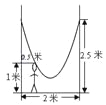
0.5
【解析】试题分析：首先以点名所在的直线为x轴，最低点所在的直线为y轴建立平面直角坐标系，然后求出二次函数的解析式，最后计算出顶点坐标，顶点坐标的纵坐标就是距离地面的距离. 如图，正方形ABCD的边长为1，E、F分别是边BC和CD上的动点（不与正方形的顶点重合），不管E、F怎样动，始终保持AE⊥EF．设BE=x，DF=y，则y是x的函数，函数关系式是（ ）
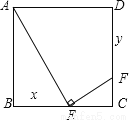
A. y=x+1 B. y=x-1 C. y=x2-x+1 D. y=x2-x-1
C
【解析】试题分析：易证△ABE∽△ECF，根据相似三角形对应边的比相等即可求解．
【解析】
∵∠BAE和∠EFC都是∠AEB的余角．
∴∠BAE=∠FEC．
∴△ABE∽△ECF
那么AB：EC=BE：CF，
∵AB=1，BE=x，EC=1﹣x，CF=1﹣y．
∴AB•CF=EC•BE，
即1×（1﹣y）=（1﹣x）x．
化简得：y=x2... 直线y=3x-3与抛物线y=x2 －x+1的交点的个数是________ .
1
【解析】【解析】
假设直线y=3x﹣3与抛物线y=x2﹣x+1有交点，则3x﹣3=x2﹣x+1，x2﹣4x+4=0，∵△=16﹣16=0，∴方程有两个相等的实数根，∴直线y=3x﹣3与抛物线y=x2﹣x+1有1个交点．
故答案为：1． 如图，如果某个斜坡AB的长度为10米，且该斜坡最高点A到地面BC的铅垂高度为8米，求该斜坡的坡比
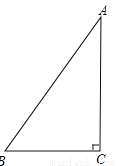
【解析】试题分析：首先根据AB和AC的长度以及勾股定理得出BC的长度，最后根据坡比的计算法则得出答案．
试题解析：∵某个斜坡AB的长度为10米，且该斜坡最高点A到地面BC的铅垂高度为8米，
∴水平距离BC= =6（m），
则该斜坡的坡比是： ．