题目内容
等腰三角形是轴对称图形，它的对称轴是( )
A. 过顶点的直线 B. 底边上的高
C. 顶角的平分线所在的直线 D. 腰上的高所在的直线
C
【解析】等腰三角形的对称轴为顶角平分线所在的直线，
故选C．
练习册系列答案
相关题目
将点A(1，－3)沿x轴向左平移3个单位长度，再沿y轴向上平移5个单位长度后得到的点A′的坐标为____．
(－2，2)．
【解析】∵点A（1，﹣3）沿x轴向左平移3个单位长度，再沿y轴向上平移5个单位长度后得到点A′，∴点A′的横坐标为1﹣3=﹣2，纵坐标为﹣3+5=2，∴A′的坐标为（﹣2，2）．故答案为：（﹣2，2）． 下列各式中，不含因式a+1的是（ ）
A. 2a2+2a B. a2+2a+1 C. a2﹣1 D.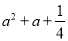 
D
【解析】A. 2a2+2a=2a(a+1) ，故不符合题意；
B. a2+2a+1=(a+1)2 ，故不符合题意；
C. a2﹣1=(a+1)(a-1) ，故不符合题意；
D. =(a+)2，故符合题意；
故选D. 一个等腰三角形的顶角为钝角，则底角a的范围是（ ）
A. 0°<a<9 B. 30°<a<90° C. 0°<a<45° D. 45°<a<90°
C
【解析】：∵等腰三角形顶角为钝角
∴顶角大于90°小于180°
∴两个底角之和大于0°小于90°
∴每个底角大于0°小于45°
故选：C 角、线段、三角形、圆、长方形和正方形中，一定是轴对称图形的有（ ）
A. 4个 B. 5个 C. 6个 D. 3个
B
【解析】通过分析可知，角、线段、圆、长方形和正方形都是轴对称图形，
故选：B. 如图，直线AB、CD被直线EF所截，∠1、∠2是同位角，如果∠1≠∠2，那么AB与CD不平行．用反证法证明这个命题时，应先假设：_____.
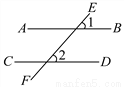
AB∥CD
【解析】试题分析：利用假设法来进行证明时，首先假设结论成立，即应先假设AB∥CD． 下列能断定△ABC为等腰三角形的是（ ）
A.∠A=30°，∠B=60° B.∠A=50°，∠B=80°
C.AB=AC=2，BC=4 D.AB=3，BC=7，周长为10
B
【解析】
试题分析：A、B根据三角形的内角和求出第三个角，可得结果；C不能组成三角形，D利用周长求出第三边即可得到答案，根据等腰三角形的判定，采用逐条分析排除的方法判断．
【解析】
A、根据三角形内角和定理得，∠C=180°﹣60°﹣30°=90°，故不是等腰三角形；
B、根据三角形内角和定理得，∠C=180°﹣50°﹣80°=50°，故是等腰三角形；
C、根据... 如图，小敏同学想测量一棵大树的高度，她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°.已知小敏同学身高(AB)为1.6m，则这棵树的高度为(结果精确到0.1m，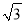 
≈1.73)( )
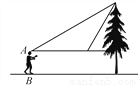
A. 3.5m B. 3.6m C. 4.3m D. 5.1m
D
【解析】如图，设CD＝xm，在Rt△ACD中，∵∠DAC＝30°，∴（m）．在Rt△ECD中，∵∠DEC＝60°，∴（m）．∵AE＝4m，∴，解得．
∴（m）．故选D． 二次函数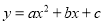
的图象如图所示，则下列结论成立的是（ ）
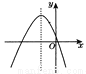
A. a＞0，bc＞0，△＜0 B. a＜0，bc＞0，△＜0
C. a＞0，bc＜0，△＜0 D. a＜0，bc＜0，△＞0
D
【解析】【解析】
∵抛物线开口向下，∴a＜0，∵对称轴x=，∴b＜0，抛物线与y轴的交点在x轴上方，∴c＞0，∴bc＜0，抛物线与x轴有两个交点，∴△＞0．故选D．