题目内容
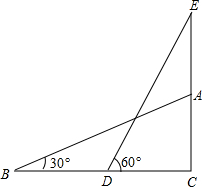 如图所示,测量楼房AC的楼顶上的电视天线AE的高度,在地面上一点B测得楼顶A的仰角为30°,前进15m,测得天线顶端E的仰角为60°,已知AC=15m,求AE的值.
如图所示,测量楼房AC的楼顶上的电视天线AE的高度,在地面上一点B测得楼顶A的仰角为30°,前进15m,测得天线顶端E的仰角为60°,已知AC=15m,求AE的值.考点:解直角三角形的应用-仰角俯角问题
专题:
分析:利用30°的正切值可得BC的值,从而得到DC的值,利用60°的正切值可得CE的值,相减即为广告牌的高度.
解答:解:∵AC=15m,
∴BC=AC÷tan30°=15
m,
∴CD=BC-BD=(15
-15)m,
∴CE=CD×tan60°=(45-15
m,
∴AE=CE-AC=45-15
-15=(30-15
)m.
答:AE的值为(30-15
)m.
∴BC=AC÷tan30°=15
| 3 |
∴CD=BC-BD=(15
| 3 |
∴CE=CD×tan60°=(45-15
| 3 |
∴AE=CE-AC=45-15
| 3 |
| 3 |
答:AE的值为(30-15
| 3 |
点评:本题考查了解直角三角形的应用,利用锐角三角函数的知识求出线段BC和CE的长,从而根据AE=CE-AC得出问题的答案是解决本题的关键.

练习册系列答案
相关题目
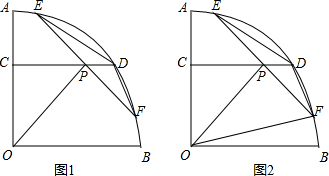 如图1,在半径为5的扇形AOB中,∠AOB=90°,点C、D分别在半径OA与弧AB上,且AC=2,CD平行OB,点P是CD上一动点,过P作PO的垂线交弧AB于点E、F,联结DE、BF.
如图1,在半径为5的扇形AOB中,∠AOB=90°,点C、D分别在半径OA与弧AB上,且AC=2,CD平行OB,点P是CD上一动点,过P作PO的垂线交弧AB于点E、F,联结DE、BF. 如图,点A、B、C的坐标分别为(-3,1)、(-4,-1)、(-1,-1),将△ABC先向下平移2个单位,得△A1B1C1;再将△A1B1C1沿y轴翻折180°,得△A2B2C2;.
如图,点A、B、C的坐标分别为(-3,1)、(-4,-1)、(-1,-1),将△ABC先向下平移2个单位,得△A1B1C1;再将△A1B1C1沿y轴翻折180°,得△A2B2C2;. 如图,在△ABC中,∠B=90°,AB=BC=6,点D在BC上,且BD:DC=1:2,若把△ABC进行折叠,使点A与点D重合,折痕为EF,点E在AB上,点F在AC上,求EC的长.
如图,在△ABC中,∠B=90°,AB=BC=6,点D在BC上,且BD:DC=1:2,若把△ABC进行折叠,使点A与点D重合,折痕为EF,点E在AB上,点F在AC上,求EC的长. 如图,一艘轮船以20海里/小时速度从南向北航行,当航行至A处时,测得小岛C在轮船的北偏东45度的方向处,航行一段时间后到达B处,此时测得小岛C在轮船的南偏东60度的方向处.若CB=40海里,则轮船航行的时间为
如图,一艘轮船以20海里/小时速度从南向北航行,当航行至A处时,测得小岛C在轮船的北偏东45度的方向处,航行一段时间后到达B处,此时测得小岛C在轮船的南偏东60度的方向处.若CB=40海里,则轮船航行的时间为