题目内容
 如图,一艘轮船以20海里/小时速度从南向北航行,当航行至A处时,测得小岛C在轮船的北偏东45度的方向处,航行一段时间后到达B处,此时测得小岛C在轮船的南偏东60度的方向处.若CB=40海里,则轮船航行的时间为
如图,一艘轮船以20海里/小时速度从南向北航行,当航行至A处时,测得小岛C在轮船的北偏东45度的方向处,航行一段时间后到达B处,此时测得小岛C在轮船的南偏东60度的方向处.若CB=40海里,则轮船航行的时间为考点:解直角三角形的应用-方向角问题
专题:
分析:作CD⊥AB于点D,根据题意得:∠A=45°,∠B=60°,然后分别在Rt△BDC中和Rt△ADC中,求得AD和BD,从而求得线段AB的长,利用路程除以速度求得航行的时间.
解答: 解:如图,作CD⊥AB于点D,
解:如图,作CD⊥AB于点D,
根据题意得:∠A=45°,∠B=60°,
在Rt△BDC中,
∵BC=40,
∴BD=20海里,CD=20
海里,
在Rt△ADC中,
∵∠A=45°,
∴CD=AD=20
,
∴AB=BD+AD=(20+20
)海里,
∵轮船的航行速度为20海里/小时,
∴航行时间为(20+20
)÷20=(1+
)小时,
故答案为:(1+
)小时.
 解:如图,作CD⊥AB于点D,
解:如图,作CD⊥AB于点D,根据题意得:∠A=45°,∠B=60°,
在Rt△BDC中,
∵BC=40,
∴BD=20海里,CD=20
| 3 |
在Rt△ADC中,
∵∠A=45°,
∴CD=AD=20
| 3 |
∴AB=BD+AD=(20+20
| 3 |
∵轮船的航行速度为20海里/小时,
∴航行时间为(20+20
| 3 |
| 3 |
故答案为:(1+
| 3 |
点评:本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出几何图形,并转化为数学知识解决.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
若
在实数范围内有意义,则x的取值范围是( )
| 1 | ||
|
| A、x<2 | B、x≠-2 |
| C、x>2 | D、x≤2 |
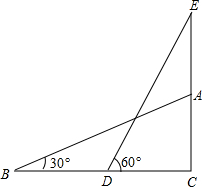 如图所示,测量楼房AC的楼顶上的电视天线AE的高度,在地面上一点B测得楼顶A的仰角为30°,前进15m,测得天线顶端E的仰角为60°,已知AC=15m,求AE的值.
如图所示,测量楼房AC的楼顶上的电视天线AE的高度,在地面上一点B测得楼顶A的仰角为30°,前进15m,测得天线顶端E的仰角为60°,已知AC=15m,求AE的值. 汽车工作时油箱中的燃油量y(升)与汽车工作时间t(小时)之间的函数图象如下中图所示,汽车开始工作时油箱中有燃油
汽车工作时油箱中的燃油量y(升)与汽车工作时间t(小时)之间的函数图象如下中图所示,汽车开始工作时油箱中有燃油