题目内容
 如图,点A、B、C的坐标分别为(-3,1)、(-4,-1)、(-1,-1),将△ABC先向下平移2个单位,得△A1B1C1;再将△A1B1C1沿y轴翻折180°,得△A2B2C2;.
如图,点A、B、C的坐标分别为(-3,1)、(-4,-1)、(-1,-1),将△ABC先向下平移2个单位,得△A1B1C1;再将△A1B1C1沿y轴翻折180°,得△A2B2C2;.(1)画出△A1B1C1和△A2B2C2;
(2)求直线A2A的解析式.
考点:作图-轴对称变换,待定系数法求一次函数解析式,作图-平移变换
专题:
分析:(1)根据平移的性质以及轴对称的性质分别得出对应点坐标求出即可;
(2)利用所画图形结合待定系数法求一次函数解析式即可.
(2)利用所画图形结合待定系数法求一次函数解析式即可.
解答: 解:(1)如图所示:△A1B1C1,△A2B2C2即为所求;
解:(1)如图所示:△A1B1C1,△A2B2C2即为所求;
(2)设直线A2A的解析式为y=kx+b
把点的坐标A(-3,1)A2的坐标(3,-1)代入上式得:
,
解得:
,
所以直线A2A的解析式为y=-
x.
 解:(1)如图所示:△A1B1C1,△A2B2C2即为所求;
解:(1)如图所示:△A1B1C1,△A2B2C2即为所求;(2)设直线A2A的解析式为y=kx+b
把点的坐标A(-3,1)A2的坐标(3,-1)代入上式得:
|
解得:
|
所以直线A2A的解析式为y=-
| 1 |
| 3 |
点评:此题主要考查了图形的平移和作轴对称变换以及待定系数法求一次函数解析式,得出对应点位置是解题关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
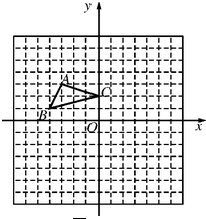 方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图.
方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图.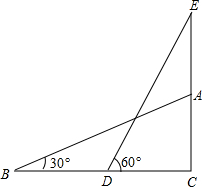 如图所示,测量楼房AC的楼顶上的电视天线AE的高度,在地面上一点B测得楼顶A的仰角为30°,前进15m,测得天线顶端E的仰角为60°,已知AC=15m,求AE的值.
如图所示,测量楼房AC的楼顶上的电视天线AE的高度,在地面上一点B测得楼顶A的仰角为30°,前进15m,测得天线顶端E的仰角为60°,已知AC=15m,求AE的值. 农场要建一个长方形的猪场,如图,有一段5米长的围墙可利用,其余部分用60米长的木栏围成.若养猪场的面积为200平方米,求养猪场的各边长.
农场要建一个长方形的猪场,如图,有一段5米长的围墙可利用,其余部分用60米长的木栏围成.若养猪场的面积为200平方米,求养猪场的各边长. 如图,在直角坐标系xOy中,直线y=mx与双曲线
如图,在直角坐标系xOy中,直线y=mx与双曲线 汽车工作时油箱中的燃油量y(升)与汽车工作时间t(小时)之间的函数图象如下中图所示,汽车开始工作时油箱中有燃油
汽车工作时油箱中的燃油量y(升)与汽车工作时间t(小时)之间的函数图象如下中图所示,汽车开始工作时油箱中有燃油