题目内容
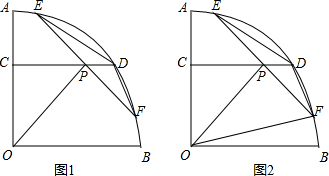 如图1,在半径为5的扇形AOB中,∠AOB=90°,点C、D分别在半径OA与弧AB上,且AC=2,CD平行OB,点P是CD上一动点,过P作PO的垂线交弧AB于点E、F,联结DE、BF.
如图1,在半径为5的扇形AOB中,∠AOB=90°,点C、D分别在半径OA与弧AB上,且AC=2,CD平行OB,点P是CD上一动点,过P作PO的垂线交弧AB于点E、F,联结DE、BF.(1)求
| S△DEP |
| S△DFP |
(2)如图2,联结EO、FO,若∠EOF=60°,求CP的长;
(3)设CP=x,△DEF的面积为y,求y关于x的函数解析式,并写出定义域.
考点:圆的综合题
专题:综合题
分析:(1)根据垂径定理可得PE=PF,继而可得
的值;
(2)首先判断∠EOP=30°,求出EP,结合AC=2求出OC,在Rt△OCP中,可求出CP的长;
(3)连结OD,作EH⊥CD,垂足为H,分别表示出OP、EP,再证明△OCP∽△PHE,利用对应边成比例求出EH,得出y的表达式即可.
| S△DEP |
| S△DFP |
(2)首先判断∠EOP=30°,求出EP,结合AC=2求出OC,在Rt△OCP中,可求出CP的长;
(3)连结OD,作EH⊥CD,垂足为H,分别表示出OP、EP,再证明△OCP∽△PHE,利用对应边成比例求出EH,得出y的表达式即可.
解答:解:(1)作DM⊥EF,垂足为M,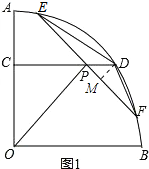
∵OP⊥EF,
∴PE=PF,
∴
=
=1.
(2)∵∠EOF=60°,
∴∠EOP=30°,
∵OE=AO=5,
∴EP=
,
∵OP⊥EF,
∴OP=
,
∵OC=OA-AC=3,
∴CP=
=
=
.
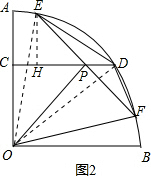 (3)连结OD,在Rt△CDO中,OC=3,OD=5,
(3)连结OD,在Rt△CDO中,OC=3,OD=5,
∴CD=4,DP=4-x,
作EH⊥CD,垂足为H,
∵OC=3,CP=x,
∴OP=
,
∴在Rt△EPO中,EP=
,
∵∠COP+∠CPO=90°,∠EPH+∠CPO=90°,
∴∠COP=∠EPH,
∴△OCP∽△PHE,
∴
=
,
∴
=
,
∴EH=
,
y=S△DEF=2S△DPE=2×
×DP×EH=(4-x)×
=
,
∴y=
(
≤x<4).

∵OP⊥EF,
∴PE=PF,
∴
| S△DEP |
| S△DFP |
| ||
|
(2)∵∠EOF=60°,
∴∠EOP=30°,
∵OE=AO=5,
∴EP=
| 5 |
| 2 |
∵OP⊥EF,
∴OP=
| 5 |
| 2 |
| 3 |
∵OC=OA-AC=3,
∴CP=
| OP2-OC2 |
|
| ||
| 2 |
 (3)连结OD,在Rt△CDO中,OC=3,OD=5,
(3)连结OD,在Rt△CDO中,OC=3,OD=5,∴CD=4,DP=4-x,
作EH⊥CD,垂足为H,
∵OC=3,CP=x,
∴OP=
| x2+9 |
∴在Rt△EPO中,EP=
| 16-x2 |
∵∠COP+∠CPO=90°,∠EPH+∠CPO=90°,
∴∠COP=∠EPH,
∴△OCP∽△PHE,
∴
| CP |
| PO |
| EH |
| EP |
∴
| x | ||
|
| EH | ||
|
∴EH=
x
| ||
|
y=S△DEF=2S△DPE=2×
| 1 |
| 2 |
x
| ||
|
(4x-x2)
| ||
|
∴y=
(4x-x2)
| ||
|
| 6 |
点评:此题考查了圆的综合,涉及了垂径定理、勾股定理、相似三角形的判定与性质,综合考察的知识点较多,解答本题关键还是基本知识的掌握,要求同学们会运用数形结合思想解题.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
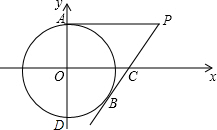 如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,D点P(2
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,D点P(2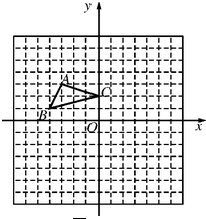 方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图.
方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图.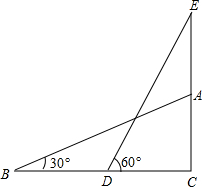 如图所示,测量楼房AC的楼顶上的电视天线AE的高度,在地面上一点B测得楼顶A的仰角为30°,前进15m,测得天线顶端E的仰角为60°,已知AC=15m,求AE的值.
如图所示,测量楼房AC的楼顶上的电视天线AE的高度,在地面上一点B测得楼顶A的仰角为30°,前进15m,测得天线顶端E的仰角为60°,已知AC=15m,求AE的值.