题目内容
3．方程x2+|x|-12=0的所有实数根之和等于0．分析 根据绝对值的性质分类讨论，再解方程求得根之后相加即可得．
解答 解：当x≥0时，方程为x2+x-12=0，即（x-3）（x+4）=0，
解得：x=3或x=-4（舍）；
当x＜0时，方程为x2-x-12=0，即（x+3）（x-4）=0，
解得：x=-3或x=4（舍），
则方程x2+|x|-12=0的所有实数根之和等于为-3+3=0，
故答案为：0．
点评 本题主要考查绝对值的性质和解方程的能力，依据绝对值的性质分类讨论是解题的关键．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
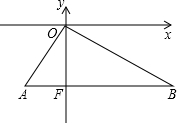如图，在平面直角坐标系中，直角三角形的直角顶点与坐标原点重合，AB⊥y轴，垂足为点F，OA=2，∠B=30°，在Rt△OAB内（包含边界）有一动点M（x，y），以M为圆心的⊙M经过原点O，且与AB边相切于点C，⊙M与边OA、OB分别交于点D、E，则DE的取值范围为$\sqrt{3}$≤DE≤$\frac{4\sqrt{3}}{3}$．
12．二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：
根据以上信息，某同学得到以下结论：①抛物线的开口向上；②当x＞-2时，y随x的增大而增大；③二次函数的最小值是-2；④抛物线的对称轴是x=-$\frac{5}{2}$，其中正确的有（ ）
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |