题目内容
14. 如图所示,现有一圆心角为90°、半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒;如果用其它铁片再做一个圆形盖子把量筒底面密封.(接缝都忽略不计).
如图所示,现有一圆心角为90°、半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒;如果用其它铁片再做一个圆形盖子把量筒底面密封.(接缝都忽略不计).求:(1)该圆锥盖子的半径为多少cm?
(2)制作这个密封量筒,共用铁片多少cm2.(注意:结果保留π)
分析 (1)根据扇形的弧长等于圆锥的底面周长,利用扇形的弧长公式即可求得圆锥的底面周长,然后根据圆的周长公式即可求解;
(2)将圆锥的底面积和侧面积相加即可.
解答 解:(1)圆锥的底面周长是:$\frac{90π×80}{180}$=40πcm.
设圆锥底面圆的半径是r,则
2πr=40π.
解得:r=20cm;
(2)S=S侧+S底=$\frac{1}{4}$×π×802+400π=2000π(cm2).
答:共用铁片2000πcm2.
点评 本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
相关题目
2.下列各数中,数值相等的是( )
| A. | 32和23 | B. | -23和(-2)3 | C. | -32和(-3)2 | D. | -(-3)和-|-3| |
6.方程x2=2x的解是( )
| A. | x1=-2,x2=0 | B. | x1=$\sqrt{2}$,x2=0 | C. | x1=1,x2=2 | D. | x1=2,x2=0 |
4.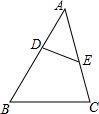 如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
 如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )| A. | 1:$\sqrt{3}$ | B. | 1:2 | C. | 1:3 | D. | 1:4 |
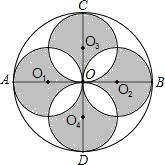 如图,AB、CD是⊙O的两条互相垂直的直径,点O1、O2、O3、O4分别OA、OB、OC、OD的中点,若⊙O的半径是4,则阴影部分的面积为32.
如图,AB、CD是⊙O的两条互相垂直的直径,点O1、O2、O3、O4分别OA、OB、OC、OD的中点,若⊙O的半径是4,则阴影部分的面积为32. 直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上在原点O处的点到达点O′,点P表示的数是2.6,那么点PO′的长度是π-2.6.
直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上在原点O处的点到达点O′,点P表示的数是2.6,那么点PO′的长度是π-2.6.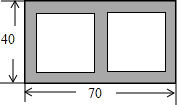 如图,在长70m,宽40m的长方形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的$\frac{1}{8}$,则路宽x应满足的方程是(70-3x)(40-2x)=40×70×(1-$\frac{1}{8}$).
如图,在长70m,宽40m的长方形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的$\frac{1}{8}$,则路宽x应满足的方程是(70-3x)(40-2x)=40×70×(1-$\frac{1}{8}$).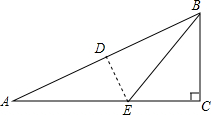 如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为12.
如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为12. 如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.
如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.