题目内容

16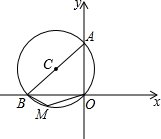．如图，⊙C过原点，且与两坐标轴分别交于点A、点B，点A的坐标为（0，4），M是第三象限内$\widehat{OB}$上一点，∠BMO=120°，则⊙C的半径长为（　　）
A．5B．4C．3D．4$\sqrt{2}$

分析 连接OC，由圆周角定理可知AB为⊙C的直径，再根据∠BMO=120°可求出∠BAO的度数，证明△AOC是等边三角形，即可得出结果．

解答 解：连接OC，如图所示，
∵∠AOB=90°，
∴AB为⊙C的直径，
∵∠BMO=120°，
∴∠BCO=120°，∠BAO=60°，
∵AC=OC，∠BAO=60°，
∴△AOC是等边三角形，
∴⊙C的半径=OA=4．
故选：B．

点评 本题考查了圆周角定理、圆内接四边形的性质、等边三角形的判定与性质；熟练掌握圆内接四边形的性质，证明三角形是等边三角形是解决问题的关键．

练习册系列答案
相关题目
18．某超市为了答谢顾客，凡在本超市购物的顾客，均可凭购物小票参与抽奖活动，奖品是三种瓶装饮料，它们分别是：绿茶、红茶和可乐，抽奖规则如下：①一个材质均匀可自由转动的转盘，转盘被等分成五个扇形区域，每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样；②参与一次抽奖活动的顾客可进行两次“有效随机转动”（当转动转盘，转盘停止后，可获得指针所指区域的字样，我们称这次转动为一次“有效随机转动”）；③假设顾客转动转盘，转盘停止后，指针指向两区域的边界，顾客可以再转动转盘，直到转动为一次“有效随机转动”；④当顾客完成一次抽奖活动后，记下两次指针所指区域的两个字，只要这两个字和奖品名称的两个字相同（与字的顺序无关），便可获得相应奖品一瓶：不相同时，不能获得任何奖品．
根据以上规则，回答下列问题：
（1）求一次“有效随机转动”可获得“乐”字的概率；
（2）有一名顾客凭本超市的购物小票，参与了一次抽奖活动，请你用列表或树状图等方法，求该顾客经过两次“有效随机转动”后，获得一瓶可乐的概率．
19．若关于x的一元二次方程kx2-4x+1=0有实数根，则k的取值范围是（　　）
A．k=4B．k＞4C．k≤4且k≠0D．k≤4
4．阅读资料：
如图1，在平面直角坐标系xOy中，A，B两点的坐标分别为A（x1，y1），B（x2，y2），由勾股定理得AB2=${{|x}_{2}{-x}_{1}|}^{2}$+${{|y}_{2}{-y}_{1}|}^{2}$，所以A，B两点间的距离为AB=$\sqrt{{{（x}_{2}{-x}_{1}）}^{2}{+{（y}_{2}{-y}_{1}）}^{2}}$．
我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系xOy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA2=|x-0|2+|y-0|2，当⊙O的半径为r时，⊙O的方程可写为：x2+y2=r2．
问题拓展：如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为（x-a）2+（y-b）2=r2．
综合应用：如图3，⊙P与x轴相切于原点O，P点坐标为（0，3），A是⊙P上一点，连接OA，使tan∠POA=$\frac{3}{4}$，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．问：是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以Q为圆心，以OQ为半径的⊙O的方程；若不存在，说明理由．
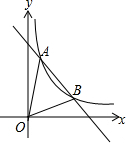11．如图，已知反比例函数y=kx-1（k＞0）的图象与一次函数图象y=-x+4交于a、b两点，点a的纵坐标为3．
（1）求反比例函数的解析；
（2）y轴上是否存在一点P，使2∠APB=∠AOB？若存在，求出点P的坐标；若不存在，请说明理由．
1．若二次函数y=ax2-2ax-1，当x分别取x1．x2两个不同的值时，函数值相等，则当x取x1+x2时，函数值为-1．
8．如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F，另一边交CB的延长线于点C．

（1）求证：EF=EG；
（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变．
①（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；
②若EC=2，试求四边形EFCG的面积．
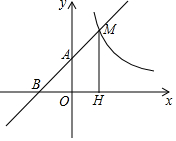5．如图，直线y=x+1与x轴交于点B，y轴交于A点，与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点M，过M作MH⊥x轴于点H，且AO=$\frac{1}{2}$MH．
（1）求k的值；
（2）在y轴上是否存在点P，使得点P、A、H、M为顶点的四边形是平行四边形？若存在，求出P点坐标；若不存在，请说明理由．
6．如图，已知矩形OABC的面积为50，它的对角线OB与双曲线y=$\frac{k}{x}$相交于点D，且OD：OB=3：5，则k=-18．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网