题目内容
6. 如图,已知矩形OABC的面积为50,它的对角线OB与双曲线y=$\frac{k}{x}$相交于点D,且OD:OB=3:5,则k=-18.
如图,已知矩形OABC的面积为50,它的对角线OB与双曲线y=$\frac{k}{x}$相交于点D,且OD:OB=3:5,则k=-18.
分析 作DE⊥OA,DF⊥OC.则矩形ABCO∽矩形EDFO,依据相似图形的面积比等于相似比的平方可得到矩形EDFO的面积,然后依据反比例函数图象位于第二象限可求得k的值.
解答 解:如图所示:作DE⊥OA,DF⊥OC.则矩形ABCO∽矩形EDFO.
∴矩形ABCO的面积:矩形EDFO的面积=25:9,即50:矩形EDFO的面积=25:9,
∴矩形EDFO的面积=18.
∵反比例函数图象位于第二象限,
∴k=-18.
故答案为:-18.
点评 本题主要考查的是反比例函数系数k的几何意义,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
16.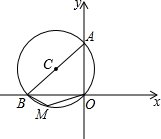 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,4),M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径长为( )
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,4),M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径长为( )
 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,4),M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径长为( )
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,4),M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径长为( )| A. | 5 | B. | 4 | C. | 3 | D. | 4$\sqrt{2}$ |
18.式子$\sqrt{x-1}$成立的条件是( )
| A. | x≥1 | B. | x>1 | C. | x<-1 | D. | x≤-1 |
15.今年元月份李老师到银行开户,存入3000元钱,以后的每月根据收入情况存入一笔钱,下表为李老师从2月份到7月份的存款情况:(超出上月记为正)
根据记录,从2月份至7月份中4月份存入的钱最多,7月份存入的钱最少,截至七月份,存折上共有21950元.
| 月份 | 2 | 3 | 4 | 5 | 6 | 7 |
| 与上一月比较(元) | -200 | +450 | +400 | -300 | -100 | -600 |
 如图,?ABCD中,∠B=45°,AC⊥BC,E是CA延长线上一点,O是AB的中点,连接OE,交DA延长线与点H,过点O作OG⊥OE交AC于点F,交BC的延长线于点G,连接CO.
如图,?ABCD中,∠B=45°,AC⊥BC,E是CA延长线上一点,O是AB的中点,连接OE,交DA延长线与点H,过点O作OG⊥OE交AC于点F,交BC的延长线于点G,连接CO.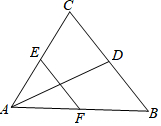 已知:如图,在△ABC中,D、E、F是分别是三边BC、AC、AB的中点,连接EF、AD.
已知:如图,在△ABC中,D、E、F是分别是三边BC、AC、AB的中点,连接EF、AD.