题目内容
20.已知二次函数y=-x2+6x-8.求:(1)用配方法将解析式化为顶点式,写出顶点坐标对称轴;
(2)画出此抛物线图象,利用图象回答下列问题:
①方程x2-6x十8=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
(3)将抛物线经过怎样的平移与坐标轴有两个交点,写出平移方法及平移后的解析式.(写出一种即可)
分析 (1)利用配方的方法,将二次函数解析式变为顶点式;
(2)画出抛物线图象,根据图象即可得出结论;
(3)若要与坐标轴只有两个交点,只需抛物线与x轴相切即可,最简单的办法直接往下平移一个单位.
解答 解:(1)∵二次函数y=-x2+6x-8=-(x2-6x+9)+1=-(x-3)2+1.
∴抛物线的顶点为(3,1),对称轴为x=3.
(2)画出图象,如下图,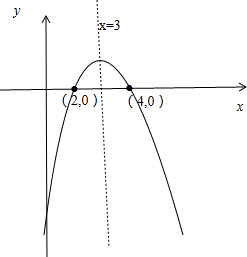
①方程x2-6x十8=0的解是x=2或x=4.
②当2<x<4时,函数值大于0.
③当x<2,或x>4时,函数值小于0.
(3)若要抛物线与坐标轴只有两个交点,抛物线与x轴相切即可.
将抛物线向下平移1个单位即可,此时抛物线的解析式为y=-(x-3)2═-x2+6x-9.
点评 本题考查了二次函数的性质以及二次函数的图象,解题的关键是:(1)利用配方法将二次函数解析式变为顶点式;(2)画出抛物线图象;(3)若与对称轴只有两个交点,只能相交.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
8.已知函数y=$\frac{k}{x}$(k≠0)的图象过点(a,b),则它必经过的另一点是( )
| A. | (a,-b) | B. | (-a,b) | C. | (-b,a) | D. | (b,a) |
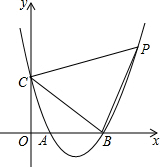 如图,抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P为对称轴右侧的抛物线上一点,若tan∠PCB=2,求P点坐标.
如图,抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P为对称轴右侧的抛物线上一点,若tan∠PCB=2,求P点坐标. 已知,如图,AD是△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:AB=AC.
已知,如图,AD是△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:AB=AC.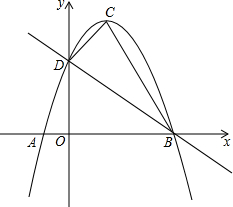 如图,抛物线y=ax2+bx+c的顶点为C(1,4),且与y轴交于点D(0,3),与x轴交于A、B两点.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),且与y轴交于点D(0,3),与x轴交于A、B两点. 已知抛物线y=x2+ax+a-2.
已知抛物线y=x2+ax+a-2. 如图所示,已知△ABC中AD,BE分别是BC,AC的高,且BD=AD.求证:
如图所示,已知△ABC中AD,BE分别是BC,AC的高,且BD=AD.求证: