题目内容
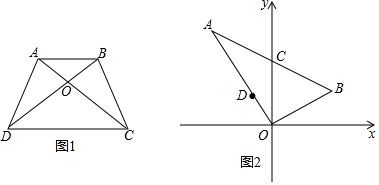
1.(1)如图1,梯形ABCD中对角线交于点O,AB∥CD,请写出图中面积相等的三角形;(2)如图2,在直角坐标系中,O是坐标原点,点A(-2,3),B(2,1).
①分别求三角形ACO和三角形BCO的面积及点C的坐标;
②请利用(1)的结论解决如下问题:D是边OA上一点,过点D作直线DE平分三角形ABO的面积,并交AB于点E(要有适当的作图说明).
分析 (1)根据同底等高面积相等,即可解决问题;
(2)①求出直线AB的解析式可得点C坐标,即可解决问题;
②连接CD,过点O作OE∥CD交AB于点E,连接DE,则DE就是所作的线.
解答 解:(1)∵AB∥DC,
∴S△ABD=S△ABC,S△ADC=S△BDC,
∴S△AOD=S△BOC.
(2)∵点A(-2,3),B(2,1),
∴直线AB的解析式为y=-$\frac{1}{2}$x+2,
∴C(0,2)
∴S△AOC=$\frac{1}{2}$×2×2=2,S△BOC=$\frac{1}{2}$×2×2=2,
,
(3)连接CD,过点O作OE∥CD交AB于点E,连接DE,则DE就是所作的线.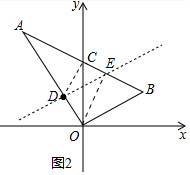
点评 本题考查梯形,坐标与图形的性质,一次函数的应用,等高模型等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列四个不等式组中,解为-1<x<3的不等式组有可能是( )
| A. | $\left\{{\begin{array}{l}{ax>1}\\{bx>1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{ax<2}\\{bx<2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{ax>3}\\{bx<3}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{ax<4}\\{bx>4}\end{array}}\right.$ |
13.正方形ABCD,过B作直线l平行于AC,在l上找一点F,使AF=AC,则∠CAF的度数为( )
| A. | 15° | B. | 30° | C. | 30°或60° | D. | 30°或150° |
 “某市道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过60千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米C处,过了2秒后到达B处,测得小汽车与车速检测仪间距离为50米,请问这辆小汽车超速了吗?为什么?若超速,则超速了多少?
“某市道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过60千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米C处,过了2秒后到达B处,测得小汽车与车速检测仪间距离为50米,请问这辆小汽车超速了吗?为什么?若超速,则超速了多少?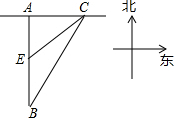 阅读材料,回答问题
阅读材料,回答问题