题目内容
6.计算或化简(1)(-$\frac{2}{3}$a2b)3÷(-$\frac{1}{3}$a2b)2×$\frac{3}{4}$a3b2
(2)(2+1)×(22+1)×(24+1)×(28+1)×(216+1)×(232+1)
分析 (1)首先计算乘方,然后计算除法和乘法,求出算式的值是多少即可.
(2)算式的左边乘2-1,应用平方差公式,求出算式的值是多少即可.
解答 解:(1)(-$\frac{2}{3}$a2b)3÷(-$\frac{1}{3}$a2b)2×$\frac{3}{4}$a3b2
=-$\frac{8}{27}$a6b3÷$\frac{1}{9}$a4b2×$\frac{3}{4}$a3b2
=-$\frac{8}{3}$a2b×$\frac{3}{4}$a3b2
=-2a5b3
(2)(2+1)×(22+1)×(24+1)×(28+1)×(216+1)×(232+1)
=(2-1)(2+1)×(22+1)×(24+1)×(28+1)×(216+1)×(232+1)
=(22-1)×(22+1)×(24+1)×(28+1)×(216+1)×(232+1)
=(24-1)×(24+1)×(28+1)×(216+1)×(232+1)
=(28-1)×(28+1)×(216+1)×(232+1)
=(216-1)×(216+1)×(232+1)
=(232-1)×(232+1)
=264-1
点评 此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
16.如果一个三角形的三条高的交点恰好是三角形的一个顶点,则这个三角形的形状一定是( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 直角三角形 |
17.在方格纸中,每个方格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图甲中,每个小正方形的边长为1,以线段AB为一边的格点三角形随着第三个顶点的位置不同而发生变化.
(1)根据图甲,填写下表,并计算出格点三角形面积的平均值.
(2)在图乙中,所给的方格纸大小与甲图一样,如果以线段CD为一边,做格点三角形,试填写下表,并计算出格点三角形面积的平均值.
(3)如果将图乙中格点三角形的面积用y来表示,频数用x来表示,根据你所填写的数据,猜想y与x之间存在何种函数关系?并求出该函数关系.
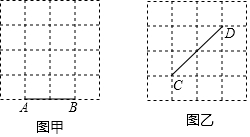
(1)根据图甲,填写下表,并计算出格点三角形面积的平均值.
| 格点三角形面积 | 1 | 2 | 3 | 4 |
| 频数 | 5 | 5 | 5 | 5 |
(3)如果将图乙中格点三角形的面积用y来表示,频数用x来表示,根据你所填写的数据,猜想y与x之间存在何种函数关系?并求出该函数关系.

 如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,求:
如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,求: