题目内容
9.给定下面一列分式:$\frac{2}{a-1}$,$-\frac{4b}{{{{({a-1})}^2}}}$,$\frac{{6{b^2}}}{{{{({a-1})}^3}}}$,$-\frac{{8{b^3}}}{{{{({a-1})}^4}}}$,…(其中a≠1)(1)请写出第6个分式;
(2)当3a-4b=3时,求$\frac{{6{b^2}}}{{{{({a-1})}^3}}}-\frac{{8{b^3}}}{{{{({a-1})}^4}}}$的值.
分析 (1)根据已知分式的特点直接写出第6个即可;
(2)把已知等式两边除以3,变形后整体代入化简即可.
解答 解:(1)第6个分式为:-$\frac{12b}{(a-1)^{2}}$;
(2)由3a-4b=3可得:a-1=$\frac{4b}{3}$,
把a-1=$\frac{4b}{3}$代入$\frac{{6{b^2}}}{{{{({a-1})}^3}}}-\frac{{8{b^3}}}{{{{({a-1})}^4}}}$=$\frac{6{b}^{2}}{(\frac{4b}{3})^{2}}$-$\frac{8{b}^{3}}{(\frac{4b}{3})^{3}}$=$\frac{27}{8}$-$\frac{27}{8}$=0.
点评 此题主要考查分式的规律探索和分式的化简,会根据题意进行适当变形整体代入是解题的关键.

练习册系列答案
相关题目
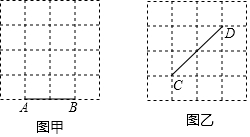
17.在方格纸中,每个方格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图甲中,每个小正方形的边长为1,以线段AB为一边的格点三角形随着第三个顶点的位置不同而发生变化.
(1)根据图甲,填写下表,并计算出格点三角形面积的平均值.
(2)在图乙中,所给的方格纸大小与甲图一样,如果以线段CD为一边,做格点三角形,试填写下表,并计算出格点三角形面积的平均值.
(3)如果将图乙中格点三角形的面积用y来表示,频数用x来表示,根据你所填写的数据,猜想y与x之间存在何种函数关系?并求出该函数关系.
(1)根据图甲,填写下表,并计算出格点三角形面积的平均值.
| 格点三角形面积 | 1 | 2 | 3 | 4 |
| 频数 | 5 | 5 | 5 | 5 |
(3)如果将图乙中格点三角形的面积用y来表示,频数用x来表示,根据你所填写的数据,猜想y与x之间存在何种函数关系?并求出该函数关系.

4.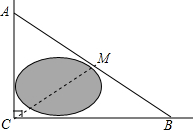 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得
AM的长为1.2km,则M,C两点间的距离为( )
 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
| A. | 0.5 km | B. | 0.6 km | C. | 0.9 km | D. | 1.2 km |
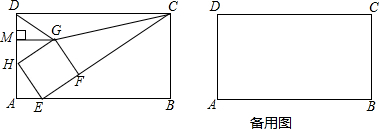
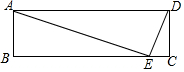 如图,在矩形ABCD中,E为BC上一点,AE⊥DE,∠DAE=30°,若DE=m+n.且m,n满足m=$\sqrt{n-8}$+$\sqrt{16-2n}$+2.则BE的长为15.
如图,在矩形ABCD中,E为BC上一点,AE⊥DE,∠DAE=30°,若DE=m+n.且m,n满足m=$\sqrt{n-8}$+$\sqrt{16-2n}$+2.则BE的长为15.