题目内容
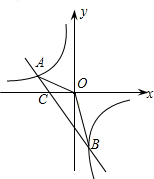 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=| m |
| x |
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)直接写出kx+b>
| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)先把B点坐标代入代入y=
求出m得到反比例函数解析式,再利用反比例函数解析式确定A点坐标,然后利用待定系数法求一次函数解析式;
(2)根据x轴上点的坐标特征确定C点坐标,然后根据三角形面积公式和△AOB的面积=S△AOC+S△BOC进行计算;
(3)观察函数图象得到当x<-4或0<x<2时,一次函数图象都在反比例函数图象上方.
| m |
| x |
(2)根据x轴上点的坐标特征确定C点坐标,然后根据三角形面积公式和△AOB的面积=S△AOC+S△BOC进行计算;
(3)观察函数图象得到当x<-4或0<x<2时,一次函数图象都在反比例函数图象上方.
解答:解:(1)把B(2,-4)代入y=
得m=2×(-4)=-8,
所以反比例函数解析式为y=-
,
把A(-4,n)代入y=-
得-4n=-8,解得n=2,则A点坐标为(-4,2),
把A(-4,2),B(2,-4)分别代入y=kx+b得
,解得
,
所以一次函数的解析式为y=-x-2;
(2)当y=0时,-x-2=0,解得x=-2,则C点坐标为(-2,0),
所以△AOB的面积=S△AOC+S△BOC
=
×2×2+
×2×4
=6;
(3)x<-4或0<x<2.
| m |
| x |
所以反比例函数解析式为y=-
| 8 |
| x |
把A(-4,n)代入y=-
| 8 |
| x |
把A(-4,2),B(2,-4)分别代入y=kx+b得
|
|
所以一次函数的解析式为y=-x-2;
(2)当y=0时,-x-2=0,解得x=-2,则C点坐标为(-2,0),
所以△AOB的面积=S△AOC+S△BOC
=
| 1 |
| 2 |
| 1 |
| 2 |
=6;
(3)x<-4或0<x<2.
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
相关题目
 把六张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为acm,宽为bcm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
把六张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为acm,宽为bcm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )| A、4bcm |
| B、(3a+b)cm |
| C、(2a+2b)cm |
| D、(a+3b)cm |
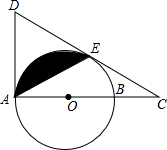 如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.
如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.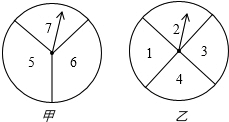 如图,两个转盘中指针落在每一个数字上的机会均等,转动甲、乙两个转盘,转盘停止后指针将各指向一个数字.
如图,两个转盘中指针落在每一个数字上的机会均等,转动甲、乙两个转盘,转盘停止后指针将各指向一个数字.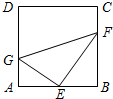 如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )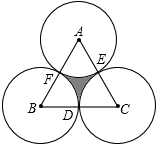 如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为
如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为