题目内容
计算:
.
|
考点:二次根式的性质与化简
专题:
分析:把98×99×100×101+1化为98992,再求解即可.
解答:解:98×99×100×101+1
=98×(98+1)×(98+2)×(98+3)+1
=[98×(98+3)]×[(98+1)×(98+2)]+1
=(982+3×98)×[(982+3×98)+2]+1
=(982+3×98)2+2×(982+3×98)+1,
=[(982+3×98)+1]2
=[98×(98+2)+98+1]2
=(98×100+99)2
=98992
所以
=
×9899=4949.5.
=98×(98+1)×(98+2)×(98+3)+1
=[98×(98+3)]×[(98+1)×(98+2)]+1
=(982+3×98)×[(982+3×98)+2]+1
=(982+3×98)2+2×(982+3×98)+1,
=[(982+3×98)+1]2
=[98×(98+2)+98+1]2
=(98×100+99)2
=98992
所以
|
| 1 |
| 2 |
点评:本题主要考查了二次根式的化简与求值,解题的关键是把98×99×100×101+1化为完全平方的形式.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
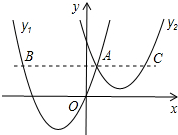 如图,抛物线y1=a(x+2)2-3与y2=
如图,抛物线y1=a(x+2)2-3与y2=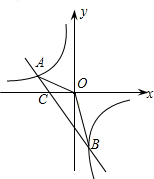 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y= 如图,AD∥BE∥FC,它们依次交直线l1、l2于点A、B、C和点D、E、F.如果AB=2,BC=3,那么
如图,AD∥BE∥FC,它们依次交直线l1、l2于点A、B、C和点D、E、F.如果AB=2,BC=3,那么