题目内容
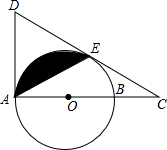 如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.
如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.(1)求证:AB=2BC;
(2)若AB=4cm,求图中阴影部分(弓形)的面积.(结果保留根号)
考点:切线的性质,扇形面积的计算
专题:
分析:(1)连接OE、BE,根据切线的性质得出AD=DE,进而得出∠DAE=∠DEA,根据已知求得∠EAC=∠C,从而求得∠DAE=∠DEA=2∠EAC,进而求得∠EAC=30°,求得AB=2BE,然后求得BE=BC,即可求得结论;
(2)根据勾股定理求得AE,AE边上的高OF,然后根据S阴影=S扇形-S△AOE即可求得.
(2)根据勾股定理求得AE,AE边上的高OF,然后根据S阴影=S扇形-S△AOE即可求得.
解答: 解:(1)连接OE、BE,
解:(1)连接OE、BE,
∵AD、DC是⊙O的切线,
∴AD=DE,
∴∠DAE=∠DEA,
∵AE=CE,
∴∠EAC=∠C,
∴∠DAE=∠DEA=2∠EAC,
∵∠DAE+∠EAC=∠DAC=90°,
∴∠EAC=30°,
∵AB是直径,
∴∠AEB=90°,
∴AB=2BE,
∵DC是⊙O的切线,
∴∠BEC=∠EAC,
∴∠BEC=∠C,
∴BE=BC,
∴AB=2BC.
(2)作OF⊥AE于F,
∴OF=
OA=1,
∵OA=OE=2,
∴∠EAC=∠AEO=30°,
∴∠AOE=120°,
∵AB=4,
∴BE=2,AE=
×4=2
∴OF=1,
∴S阴影=S扇形-S△AOE=
-
×2
×1=
.
 解:(1)连接OE、BE,
解:(1)连接OE、BE,∵AD、DC是⊙O的切线,
∴AD=DE,
∴∠DAE=∠DEA,
∵AE=CE,
∴∠EAC=∠C,
∴∠DAE=∠DEA=2∠EAC,
∵∠DAE+∠EAC=∠DAC=90°,
∴∠EAC=30°,
∵AB是直径,
∴∠AEB=90°,
∴AB=2BE,
∵DC是⊙O的切线,
∴∠BEC=∠EAC,
∴∠BEC=∠C,
∴BE=BC,
∴AB=2BC.
(2)作OF⊥AE于F,
∴OF=
| 1 |
| 2 |
∵OA=OE=2,
∴∠EAC=∠AEO=30°,
∴∠AOE=120°,
∵AB=4,
∴BE=2,AE=
| ||
| 2 |
| 3 |
∴OF=1,
∴S阴影=S扇形-S△AOE=
| 120×π×22 |
| 360 |
| 1 |
| 2 |
| 3 |
4π-3
| ||
| 3 |
点评:本题考查了切线的性质,等腰三角形的性质勾股定理的应用,30°角的直角三角形的性质等,作出辅助线构建直角三角形和等腰三角形是本题的关键.

练习册系列答案
相关题目
若n为正整数,则计算(-2)2n+1+2×(-2)2n的结果是( )
| A、0 |
| B、1 |
| C、22n+1 |
| D、-22n+1 |
 如图是一个正方体的平面展开图,则原正方体中“中”字所在的面相对的面上标的字是( )
如图是一个正方体的平面展开图,则原正方体中“中”字所在的面相对的面上标的字是( )| A、爱 | B、伟 | C、国 | D、美 |
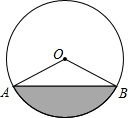 下图是输水管的切面,阴影部分是有水部分,其中水面AB宽16cm,水最深4cm.
下图是输水管的切面,阴影部分是有水部分,其中水面AB宽16cm,水最深4cm. 如图,抛物线y1=a(x+2)2-3与y2=
如图,抛物线y1=a(x+2)2-3与y2= 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y= 如图,已知抛物线y=
如图,已知抛物线y=