题目内容
9.已知$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,则方程组$\left\{\begin{array}{l}{3{a}_{1}(x-1)+4{b}_{1}(y+3)={c}_{1}}\\{3{a}_{2}(x-1)+4{b}_{2}(y+3)={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$.分析 根据二元一次方程组的解,即可解答.
解答 解:将$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$代入$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$得:$\left\{\begin{array}{l}{3{a}_{1}+4{b}_{1}={c}_{1}}\\{3{a}_{2}+4{b}_{2}={c}_{2}}\end{array}\right.$,
将$\left\{\begin{array}{l}{3{a}_{1}+4{b}_{1}={c}_{1}}\\{3{a}_{2}+4{b}_{2}={c}_{2}}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{3{a}_{1}(x-1)+4{b}_{1}(y+3)={c}_{1}}\\{3{a}_{2}(x-1)+4{b}_{2}(y+3)={c}_{2}}\end{array}\right.$得:
$\left\{\begin{array}{l}{x-1=1}\\{y+3=1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$.
点评 本题考查了二元一次方程组的解,解决本题的关键是解二元一次方程组.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
2.方程x2-2x+3=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个不相等的实数根 | D. | 只有一个实数根 |
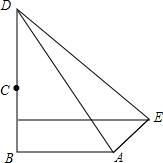 已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)
已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)