题目内容
8．在△ABC中，AB=AC=17，BC=16，则△ABC的面积为（ ）| A． | 60 | B． | 80 | C． | 100 | D． | 120 |
分析 利用等腰三角形的性质求得BD=$\frac{1}{2}$BC=8．然后在直角△ABD中，利用勾股定理来求AD的长度，进而可求出三角形的面积．
解答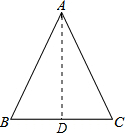 
解：如图，作AD⊥BC于点D，
∵△ABC中，AB=AC=17，BC=16，
∴BD=$\frac{1}{2}$BC=8，
∴在直角△ABD中，由勾股定理，得AD=$\sqrt{1{7}^{2}-{8}^{2}}$=15，
∴S△ABC=$\frac{1}{2}$×15×16=120，
故选：D．
点评 此题主要考查了勾股定理，等腰三角形的性质的理解及运用．利用等腰三角形“三线合一”的性质求得AD的长度是解题的关键．
练习册系列答案
相关题目
如图，正方形ABCD的边长为2，将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动，如果Q点从A点出发，沿图中所示方向按A→B→C→D→A滑动到A止，同时点R从B点出发，沿图中所示方向按B→C→D→→B滑动到B止，在这个过程中，线段QR的中点M所经过的路线围成的图形的面积为（ ）