题目内容
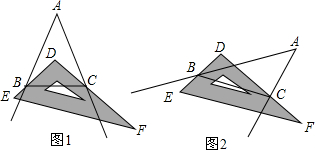
14.如图,∠BAC=40°,射线AB,AC分别交直角三角板DEF的两条直角边DE,DF于点B,C,连结BC.(1)如图1,当点D在∠BAC内部时,求∠ABD+∠ACD的度数;
(2)如图2,当点D在∠BAC外部时,求∠ACD-∠ABD的度数.
分析 (1)本题考查的是三角形内角和定理.已知∠BAC=40°易求∠ABC+∠ACB的度数.又因为∠D为90°,所以易求∠DBC+∠DCB,相减即可求出∠ABD+∠ACD;
(2)根据∠D+∠DBA=∠A+∠ACD,进而得出∠ACD-∠DBA的度数.
解答 解:(1)∵∠BAC=40°,
∴∠ABC+∠ACB=140°,
∵∠D=90°,
∴∠DBC+∠DCB=90°,
∴∠DBA+∠DCA=140°-90°=50°;
(2)∵∠D+∠DBA=∠A+∠ACD,∠D=90°,
∴90°+∠DBA=40°+∠ACD,
∴∠ACD-∠DBA=50°.
点评 考查了三角形内角和定理,此题注意运用整体法计算.关键是求出∠ABC+∠ACB.

练习册系列答案
相关题目
10.计算(-48)÷(-12)的结果是( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | -$\frac{1}{4}$ |
3.某市电力公司为了鼓励居民节约用电,采用分段计费的方法计算电费:每月用电不超过100度时,按每度0.37元计费;每月用电超过100度时,其中超过部分按每度0.50元计费.
(1)用电x度时,应交电费y元,当x≤100和x>100时,分别写出y关于x的关系式.
(2)小王家第一季度交纳电费如下:
问小王家第一季度共用电多少度?
(1)用电x度时,应交电费y元,当x≤100和x>100时,分别写出y关于x的关系式.
(2)小王家第一季度交纳电费如下:
| 月 份 | 一月份 | 二月份 | 三月份 | 四月份 |
| 交费金额 | 76元 | 63元 | 45元6角 | 184元6角 |
 已知直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的横坐标为$\sqrt{3}$
已知直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的横坐标为$\sqrt{3}$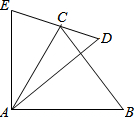 如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B.
如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B.