题目内容
8.(1)计算:$\sqrt{12}$-2cos30°+${(\sqrt{3}-1)}^{0}$-${(\frac{1}{8})}^{-1}$(2)解关于x的不等式组$\left\{\begin{array}{l}{2x+7<3x}\\{\frac{x+1}{5}-\frac{x-1}{4}≥0}\end{array}\right.$.
分析 (1)原式第一项化为最简二次根式,第二项利用特殊角的三角函数值计算,第三项利用零指数幂法则计算,最后一项利用负整数指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)原式=2$\sqrt{3}$-2×$\frac{\sqrt{3}}{2}$+1-8=$\sqrt{3}$-7;
(2)$\left\{\begin{array}{l}{2x+7<3x①}\\{\frac{x+1}{5}-\frac{x-1}{4}≥0②}\end{array}\right.$,
由①得:x>7,
由②得:x≤9,
则不等式组的解集为7<x≤9.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.计算(-$\frac{1}{2}$b2+2a)2等于( )
| A. | $\frac{1}{4}$b2-2ab2-4a2 | B. | $\frac{1}{4}$b4-2ab2+4a2 | C. | $\frac{1}{4}$b2ab2+4a2 | D. | -$\frac{1}{4}$b4+ab2-4a2 |
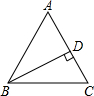 如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.
如图,△ABC中,∠ABC:∠C=5:7,∠C比∠A大10°,BD是△ABC的高,求∠A与∠CBD的度数.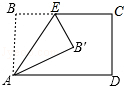 将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=60°,则∠AEB′的正切值=$\sqrt{3}$.
将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=60°,则∠AEB′的正切值=$\sqrt{3}$.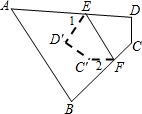 如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.
如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.