题目内容
6.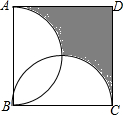 如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位.
如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位.
分析 先判断出两半圆交点为正方形的中心,连接OB,则可得出所产生的四个小弓形的面积相等,继而根据阴影部分的面积=Rt△ADC-2个小弓形的面积可得出答案.
解答 解:易知:两半圆的交点即为正方形的中心,设此点为O,连接AC,则AC必过点O,连接OB;
则图中的四个小弓形的面积相等,
∴两个半圆的面积-Rt△ABC的面积=4个小弓形的面积,
∴两个小弓形的面积为($\frac{π}{2}$-1),
图中阴影部分的面积=Rt△ADC-2个小弓形的面积=2-($\frac{π}{2}$-1)=3-$\frac{π}{2}$.
故答案是:(3-$\frac{π}{2}$).
点评 此题考查了扇形的面积计算,解答本题的关键是得出两半圆的交点是正方形的中心,求出小弓形的面积,有一定难度,注意仔细观察图形.

练习册系列答案
相关题目
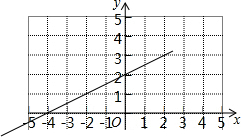 如图是某一次函数的图象,请根据图象回答问题;
如图是某一次函数的图象,请根据图象回答问题;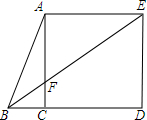 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,以AC为边向三角形外作正方形ACDE,连接BE交AC于F.若BF=$\sqrt{3}$cm,则EF=3.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,以AC为边向三角形外作正方形ACDE,连接BE交AC于F.若BF=$\sqrt{3}$cm,则EF=3.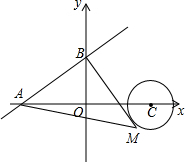 如图,已知直线y=$\frac{3}{4}$x+3与坐标轴分别交于A、B两点,M是以C(6,0)为圆心,2为半径的圆上一动点,连结MA、MB,则△MAB面积的最大值是20.
如图,已知直线y=$\frac{3}{4}$x+3与坐标轴分别交于A、B两点,M是以C(6,0)为圆心,2为半径的圆上一动点,连结MA、MB,则△MAB面积的最大值是20.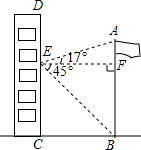 如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).
如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).