题目内容
1.关于直角三角形的可解条件,在直角三角形的六个元素中,除直角外,只要再知道2个元素(其中至少有一条边),这个三角形的形状、大小就可以确定下来,解直角三角形的基本类型可分为已知两条边(两条直角边或斜边和一条直角边)及已知一边和一个锐角(一条直角边和一个锐角或斜边和一个锐角).分析 根据勾股定理和锐角三角函数的定义可判断解直角三角形的条件.
解答 解:关于直角三角形的可解条件,在直角三角形的六个元素中,除直角外,只要再知道2个元素(其中至少有一条边),这个三角形的形状、大小就可以确定下来,解直角三角形的基本类型可分为已知两条边(两条直角边或斜边和一条直角边)及已知一边和一个锐角(一条直角边和一个锐角或斜边和一个锐角).
故答案为2个元素,有一条边,直角边,一条直角边,一条直角边,斜边.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活应用勾股定理和三角函数的定义进行计算.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.一个几何体被一个平面所截后,得到一个七边形截面,则原几何体可能是( )
| A. | 六棱柱 | B. | 正方体 | C. | 长方体 | D. | 球 |
11.填空:
| 一元二次方程 | b2-4ac的值 | 方程根的情况 |
| x2-3x-6=0 | 33 | 两个不相等的实数根 |
| x2-4x=3 | 28 | 两个不相等的实数根 |
| x2+9=6x | 0 | 两个相等的实数根 |
| -2x2=3x+2 | -7 | 没有实数根 |
| x2-2$\sqrt{2}$ | 无 | 无 |
| 2x2-3=x2-2x | 16 | 两个不相等的实数根 |
 如图,已知AB=10,点C是线段AB上一点,BC=6,点M为AB的中点,点N为BC的中点,求BN,MN的长.
如图,已知AB=10,点C是线段AB上一点,BC=6,点M为AB的中点,点N为BC的中点,求BN,MN的长.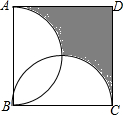 如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位.
如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位. 如图所示,在Rt△ABC中,BC=7.85,AB=11.40,解这个直角三角形.(边长保留三个有效数字,角度精确到1°)
如图所示,在Rt△ABC中,BC=7.85,AB=11.40,解这个直角三角形.(边长保留三个有效数字,角度精确到1°)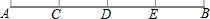 如图,点C、D、E在线段AB上,且AC=CD=DE=EB
如图,点C、D、E在线段AB上,且AC=CD=DE=EB