题目内容
11.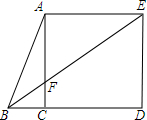 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,以AC为边向三角形外作正方形ACDE,连接BE交AC于F.若BF=$\sqrt{3}$cm,则EF=3.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,以AC为边向三角形外作正方形ACDE,连接BE交AC于F.若BF=$\sqrt{3}$cm,则EF=3.
分析 过F作FG∥BC交AB于G,根据平行线的性质得到∠AGF=∠ABC=60°,∠AFG=∠ACB=90°,由三角函数的定义得到GF=$\frac{\sqrt{3}}{3}$AF,通过△BFG∽△BAE,根据相似三角形的性质得到$\frac{GF}{AE}=\frac{BF}{BE}$,同理$\frac{CF}{DE}=\frac{BF}{BE}$,等量代换得到$\frac{GF}{AE}=\frac{CF}{DE}$,根据正方形的性质得到AC=CD=DE=AE,证得GF=CF,求出GF=$\frac{\sqrt{3}}{3+\sqrt{3}}$AC=$\frac{\sqrt{3}}{3+\sqrt{3}}$AE,即可得到结论.
解答  解:过F作FG∥BC交AB于G,
解:过F作FG∥BC交AB于G,
∴∠AGF=∠ABC=60°,∠AFG=∠ACB=90°,
∴GF=$\frac{\sqrt{3}}{3}$AF,
∵FG∥BC,
∴△BFG∽△BAE,
∴$\frac{GF}{AE}=\frac{BF}{BE}$,
同理$\frac{CF}{DE}=\frac{BF}{BE}$,
∴$\frac{GF}{AE}=\frac{CF}{DE}$,
∵四边形ACDE是正方形,
∴AC=CD=DE=AE,
∴GF=CF,
∴GF=$\frac{\sqrt{3}}{3+\sqrt{3}}$AC=$\frac{\sqrt{3}}{3+\sqrt{3}}$AE,
∵BF=$\sqrt{3}$,
∴BE=$\sqrt{3}+$3,
∴EF=3.
故答案为:3.
点评 本题考查了相似三角形的判定和性质,正方形的性质,直角三角形的性质,熟练掌握正方形的性质是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
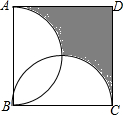 如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位.
如图,正方形ABCD的边长为2,分别以AB、BC为直径,在正方形内作半圆,则图中阴影部分的面积为(3-$\frac{π}{2}$)平方单位.
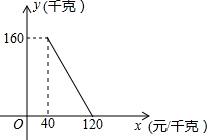 某商店以40元/千克的单价新近一批茶叶,经调查发现,在一段时间内,销量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
某商店以40元/千克的单价新近一批茶叶,经调查发现,在一段时间内,销量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.