题目内容
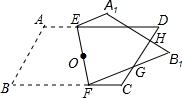 如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.考点:平行四边形的性质,翻折变换(折叠问题)
专题:证明题
分析:首先连接AC,由四边形ABCD是平行四边形,可得AD∥BC,OA=OC,又由平行线的性质,可得∠1=∠2,继而利用ASA,即可证得△AOE≌△COF,则可证得AE=CF.然后根据平行四边形的性质与折叠性质,易得A1E=CF,∠A1=∠A=∠C,∠B1=∠B=∠D,继而可证得△A1IE≌△CGF,即可证得EI=FG.
解答: 证明:连接AC,
证明:连接AC,
∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,AD=BC,
∴∠OAE=∠OCF,
∵在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴AE=CF;
由折叠的性质可得:AE=A1E,∠A1=∠A,∠B1=∠B,
∴A1E=CF,∠A1=∠A=∠C,∠B1=∠B=∠D,
又∵∠1=∠2,
∴∠3=∠4,
∵∠5=∠3,∠4=∠6,
∴∠5=∠6,
∵在△A1IE与△CGF中,
,
∴△A1IE≌△CGF(AAS),
∴EI=FG.
 证明:连接AC,
证明:连接AC,∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,AD=BC,
∴∠OAE=∠OCF,
∵在△AOE和△COF中,
|
∴△AOE≌△COF(ASA),
∴AE=CF;
由折叠的性质可得:AE=A1E,∠A1=∠A,∠B1=∠B,
∴A1E=CF,∠A1=∠A=∠C,∠B1=∠B=∠D,
又∵∠1=∠2,
∴∠3=∠4,
∵∠5=∠3,∠4=∠6,
∴∠5=∠6,
∵在△A1IE与△CGF中,
|
∴△A1IE≌△CGF(AAS),
∴EI=FG.
点评:此题考查了平行四边形的性质、折叠的性质以及全等三角形的判定与性质.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
相关题目
二次根式
中字母x的取值范围是( )
| x-1 |
| A、x<1 | B、x≤1 |
| C、x>1 | D、x≥1 |
 如图,在△ABC中,AB=AC=5,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形,DE=2,则AD=
如图,在△ABC中,AB=AC=5,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形,DE=2,则AD=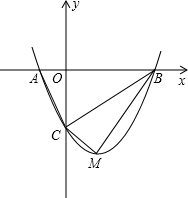 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点. 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路. 如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,
如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm, 如图,已知在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=11,BC=13,AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x.
如图,已知在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=11,BC=13,AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x.