题目内容
 如图,在△ABC中,AB=AC=5,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形,DE=2,则AD=
如图,在△ABC中,AB=AC=5,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形,DE=2,则AD=考点:平行四边形的性质,等腰三角形的判定与性质
专题:
分析:根据平行四边形的对边平行且相等可得AD=EF,AD∥EF,再根据两直线平行,同位角相等可得∠ACB=∠FEB,根据等边对等角求出∠ACB=∠B,从而得到∠FEB=∠B,然后根据等角对等边可得BF=EF,进而得到AD=BF,然后根据线段长可得答案.
解答:解:∵四边形ADEF为平行四边形,
∴AD=EF=2,AD∥EF,
∴∠ACB=∠FEB,
∵AB=AC,
∴∠ACB=∠B,
∴∠FEB=∠B,
∴EF=BF,
∴AD=BF,
∵AB=5,
∴BF=5+2=7,
∴AD=7.
故答案为:7.
∴AD=EF=2,AD∥EF,
∴∠ACB=∠FEB,
∵AB=AC,
∴∠ACB=∠B,
∴∠FEB=∠B,
∴EF=BF,
∴AD=BF,
∵AB=5,
∴BF=5+2=7,
∴AD=7.
故答案为:7.
点评:本题考查了平行四边形对边平行且相等的性质,平行线的性质,等角对等边的性质,熟练掌握各性质是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,设点C的坐标为(0,m)且m<6,△ABC的面积为S,试问:
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,设点C的坐标为(0,m)且m<6,△ABC的面积为S,试问: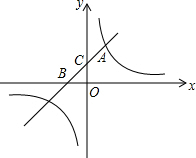 如图,已知一次函数y1=kx+b的图象与反比例函数y2=
如图,已知一次函数y1=kx+b的图象与反比例函数y2=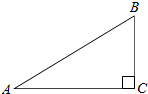 如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是
如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 如图,有两个正方形和一个等边三角形,则图中度数为30°的角有
如图,有两个正方形和一个等边三角形,则图中度数为30°的角有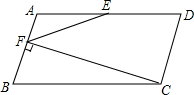 如图,在平行四边形ABCD中,BC=2AB,E为AD中点,CF⊥AB于点F,连接EF.若∠B=70°,则∠FED=
如图,在平行四边形ABCD中,BC=2AB,E为AD中点,CF⊥AB于点F,连接EF.若∠B=70°,则∠FED= 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是
如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是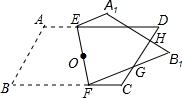 如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.