题目内容
 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
考点:解直角三角形的应用
专题:几何图形问题
分析:(1)作CH⊥AB于H.在Rt△ACH中,根据三角函数求得CH,AH,在Rt△BCH中,根据三角函数求得BH,再根据AB=AH+BH即可求解;
(2)在Rt△BCH中,根据三角函数求得BC,再根据AC+BC-AB列式计算即可求解.
(2)在Rt△BCH中,根据三角函数求得BC,再根据AC+BC-AB列式计算即可求解.
解答: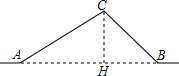 解:(1)作CH⊥AB于H.
解:(1)作CH⊥AB于H.
在Rt△ACH中,CH=AC•sin∠CAB=AC•sin25°≈10×0.42=4.2(千米),
AH=AC•cos∠CAB=AC•cos25°≈10×0.91=9.1(千米),
在Rt△BCH中,BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6(千米),
∴AB=AH+BH=9.1+5.6=14.7(千米).
故改直的公路AB的长14.7千米;
(2)在Rt△BCH中,BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7(千米),
则AC+BC-AB=10+7-14.7=2.3(千米).
答:公路改直后比原来缩短了2.3千米.
 解:(1)作CH⊥AB于H.
解:(1)作CH⊥AB于H.在Rt△ACH中,CH=AC•sin∠CAB=AC•sin25°≈10×0.42=4.2(千米),
AH=AC•cos∠CAB=AC•cos25°≈10×0.91=9.1(千米),
在Rt△BCH中,BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6(千米),
∴AB=AH+BH=9.1+5.6=14.7(千米).
故改直的公路AB的长14.7千米;
(2)在Rt△BCH中,BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7(千米),
则AC+BC-AB=10+7-14.7=2.3(千米).
答:公路改直后比原来缩短了2.3千米.
点评:此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,有两个正方形和一个等边三角形,则图中度数为30°的角有
如图,有两个正方形和一个等边三角形,则图中度数为30°的角有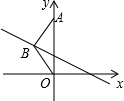 如图,等腰三角形ABO中,底边OA在y轴的正半轴上,且OA=3,点B在第二象限.若直线y=-
如图,等腰三角形ABO中,底边OA在y轴的正半轴上,且OA=3,点B在第二象限.若直线y=-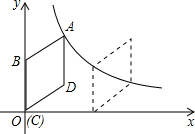 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的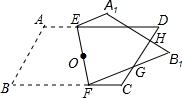 如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.