题目内容
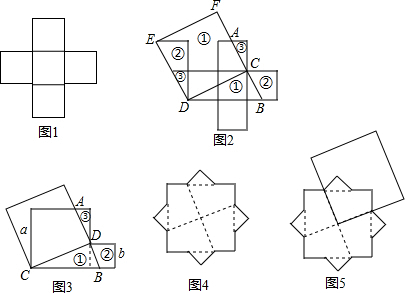
 如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,
如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,(1)求AE的长.
(2)连接BE,BE是∠ABC的平分线吗?如果是,请证明;如果不是,请说明理由.
考点:矩形的性质,全等三角形的判定与性质
专题:
分析:(1)由矩形ABCD中,EF⊥EC,且EF=EC,易证得△AEF≌△DCE,则可得AE=CD,然后设AE=CD=xcm,则AD=AE+DE=4+x(cm),由矩形ABCD的周长为32cm,可得2(x+4+x)=32,解此方程组即可求得答案;
(2)由AE=CD=AB,可得△ABE是等腰直角三角形,即可求得∠ABE=∠CBE=45°.
(2)由AE=CD=AB,可得△ABE是等腰直角三角形,即可求得∠ABE=∠CBE=45°.
解答:解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠AFE=90°,
∵EF⊥EC,
∴∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,
在△AEF和△DCE中,
,
∴△AEF≌△DCE(AAS),
∴AE=CD,
设AE=CD=xcm,则AD=AE+DE=4+x(cm),
∵矩形ABCD的周长为32cm,
∴2(x+4+x)=32,
解得:x=6,
∴AE=6cm;
(2)BE是∠ABC的平分线.
证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠ABC=90°,
∵AE=CD,
∴AE=AB,
∴∠ABE=∠AEB=45°,
∴∠CBE=45°,
∴∠ABE=∠CBE,
即BE是∠ABC的平分线.
∴∠A=∠D=90°,
∴∠AEF+∠AFE=90°,
∵EF⊥EC,
∴∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,

在△AEF和△DCE中,
|
∴△AEF≌△DCE(AAS),
∴AE=CD,
设AE=CD=xcm,则AD=AE+DE=4+x(cm),
∵矩形ABCD的周长为32cm,
∴2(x+4+x)=32,
解得:x=6,
∴AE=6cm;
(2)BE是∠ABC的平分线.
证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠ABC=90°,
∵AE=CD,
∴AE=AB,
∴∠ABE=∠AEB=45°,
∴∠CBE=45°,
∴∠ABE=∠CBE,
即BE是∠ABC的平分线.
点评:此题考查了矩形的性质、全等三角形的判定与性质以及等腰直角三角形性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
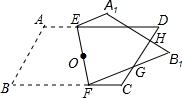 如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.