题目内容
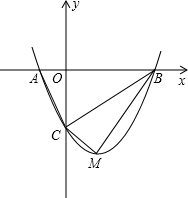 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.(1)请求出抛物线顶点M的坐标(用含m的代数式表示)及A、B两点的坐标;
(2)经探究可知,△BCM与△ABC的面积比不变,试求出这个比值;
(3)是否存在使△BCM为直角三角形的抛物线?若存在,请求出此时m的值;如果不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)直接利用配方法求出顶点坐标,当y=0,进而求出x的值,得出A,B点坐标;
(2)利用S△BCM=SBDM+SOCMD-S△OBC,分别表示出两三角形的面积,进而求出即可;
(3)分别利用①当∠BMC=90°时,②当∠BCM=90°时,③当∠CBM=90°时,分别求出即可.
(2)利用S△BCM=SBDM+SOCMD-S△OBC,分别表示出两三角形的面积,进而求出即可;
(3)分别利用①当∠BMC=90°时,②当∠BCM=90°时,③当∠CBM=90°时,分别求出即可.
解答:解:(1)∵y=mx2-2mx-3m=m(x-1)2-4m.
∴M(1,-4m).
当y=0,mx2-2mx-3m=0,
解得x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)当x=0时,y=-3m,
∴C(0,-3m).
∴S△ABC=
×2×|-3m|=6m.
过点M作MD⊥x轴于点D,则OD=1,BD=2,MD=4m.
∴S△BCM=SBDM+SOCMD-S△OBC=
×2×4m+
(3m+4m)×1-
×3×3m=3m.
∴S△BCM:S△ABC=1:2.
(3)过点C作CN⊥DM于点N,则CM2=m2+1,BC2=9m2+9,BM2=16m2+4.
①当∠BMC=90°时,CM2+BM2=BC2,即1+m2+4+16m2=9m2+9,
解得:m1=
,m2=-
(舍去).
②当∠BCM=90°时,BC2+CM2=BM2,即9m2+9+m2+1=16m2+4.
解得:m1=1,m2=-1(舍去).
③当∠CBM=90°时,BC2+BM2=CM2,即9m2+9+16m2+4=m2+1.
此方程无解.
综上所述,存在m=
或m=1,存在使△BCM为直角三角形的抛物线.
∴M(1,-4m).
当y=0,mx2-2mx-3m=0,
解得x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)当x=0时,y=-3m,
∴C(0,-3m).
∴S△ABC=
| 1 |
| 2 |
过点M作MD⊥x轴于点D,则OD=1,BD=2,MD=4m.
∴S△BCM=SBDM+SOCMD-S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

∴S△BCM:S△ABC=1:2.
(3)过点C作CN⊥DM于点N,则CM2=m2+1,BC2=9m2+9,BM2=16m2+4.
①当∠BMC=90°时,CM2+BM2=BC2,即1+m2+4+16m2=9m2+9,
解得:m1=
| ||
| 2 |
| ||
| 2 |
②当∠BCM=90°时,BC2+CM2=BM2,即9m2+9+m2+1=16m2+4.
解得:m1=1,m2=-1(舍去).
③当∠CBM=90°时,BC2+BM2=CM2,即9m2+9+16m2+4=m2+1.
此方程无解.
综上所述,存在m=
| ||
| 2 |
点评:此题主要考查了二次函数综合应用以及勾股定理的应用和三角形面积求法等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
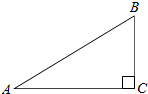 如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是
如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是
如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是
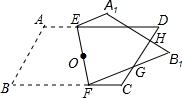 如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.