题目内容
12.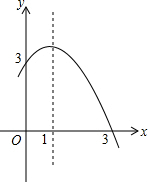 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(3,0),其部分图象如图所示,下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(3,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=-2,x2=3;
③3a+c=0;
④当y>0时,x的取值范围是-1<x<3;
⑤当x<0时,y随x增大而增大;
其中结论正确的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(3,0),则可对②进行判断;由对称轴方程得到b=-2a,然后根据x=-1时函数值为0可得到3a+c=0,则可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断;根据二次函数的性质对⑤进行判断.
解答 解:∵抛物线与x轴有2个交点,
∴b2-4ac>0,故①正确;
∵抛物线的对称轴为直线x=1,
而点(-1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=-1,x2=3,故②错误;
∵x=-$\frac{b}{2a}$=1,即b=-2a,
而x=-1时,y=0,即a-b+c=0,
∴a+2a+c=0,故③正确;
∵抛物线与x轴的两点坐标为(-1,0),(3,0),
∴当-1<x<3时,y>0,故④正确;
∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,故⑤正确.
综上所述,正确的结论有①③④⑤,共4个.
故选:A.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
20.下列说法正确的是( )
| A. | 两直线被第三条直线相截,同位角相等 | |
| B. | 相等的角是对顶角 | |
| C. | 同旁内角互补,两直线平行 | |
| D. | 互补的两个角一定有一个锐角 |
17.请借鉴以前研究函数的经验,探索函数y=$\frac{6}{x-1}$+2的图象和性质.
(1)自变量x的取值范围为x≠1;
(2)填写下表,画出函数的图象;
(3)观察图象,写出该函数两条不同类型的性质;
(4)若x>3,则y的取值范围为2<y<5;若y<-1,则x的取值范围为-1<x<1.
(1)自变量x的取值范围为x≠1;
(2)填写下表,画出函数的图象;
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| y | … | 1 | 0.8 | 0.5 | -1 | -4 | 8 |
(4)若x>3,则y的取值范围为2<y<5;若y<-1,则x的取值范围为-1<x<1.

4.为了响应节能减排的号召,推动绿色生活方式,某品牌汽车4S店准备购进A型和B型两种不同型号的电动汽车共20辆进行销售,这两款电动汽车的成本价和售价如下:
(1)如果该4S店购进20辆电动汽车所花费成本恰好为416万元,那么其中购进A型电动汽车12辆,B型电动汽车8辆;
(2)如果为了保证该4S店将购进的20辆电动汽车全部售出后,所得利润要超过19.3万元,那么A型电动汽车最多购进多少辆?
| 成本价(万元/辆) | 售价(万元/辆) | |
| A型 | 16 | 16.8 |
| B型 | 28 | 29.4 |
(2)如果为了保证该4S店将购进的20辆电动汽车全部售出后,所得利润要超过19.3万元,那么A型电动汽车最多购进多少辆?