题目内容
20．下列说法正确的是（ ）| A． | 两直线被第三条直线相截，同位角相等 | |
| B． | 相等的角是对顶角 | |
| C． | 同旁内角互补，两直线平行 | |
| D． | 互补的两个角一定有一个锐角 |
分析 根据两平行线被第三条直线相截，同位角相等；对顶角的性质：对顶角相等；同旁内角互补，两直线平行；如果两个角的和等于180°（平角），就说这两个角互为补角进行分析即可．
解答 解：A、两直线被第三条直线相截，同位角相等，说法错误；
B、相等的角是对顶角，说法错误；
C、同旁内角互补，两直线平行，说法正确；
D、互补的两个角一定有一个锐角，说法错误；
故选：C．
点评 此题主要考查了平行线的性质和判定，以及对顶角和补角，关键是掌握平行线的判定定理．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
在平面直角坐标系中，小明从原点开始，按照向上平移1个单位长度描点A1，然后向右平移2个单位长度描点A2，然后向上平移2个单位长度描点A3，然后向右平移1个单位长度描点A4，之后重复上述步骤，以此类推进行描点（如图），那么她描出的点A87的坐标是（65，66）．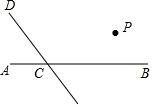
读句画图：如图，直线CD与直线AB相交于C，根据下列语句画图：
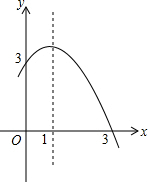如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（3，0），其部分图象如图所示，下列结论：
10．在实数$\sqrt{3}$，-2，0，$-\sqrt{2}$中，最大值是（ ）
| A． | $\sqrt{3}$ | B． | -2 | C． | 0 | D． | $-\sqrt{2}$ |