题目内容
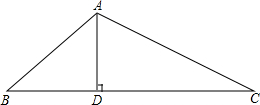 如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD=
如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD=| 3 |
| 4 |
(1)求线段AB的长;
(2)若AC=9
| 5 |
考点:解直角三角形
专题:
分析:(1)通过解直角△ABD求得BD的长度,然后在该直角三角形中利用勾股定理来求AB的长度;
(2)利用三角函数的定义进行解答.
(2)利用三角函数的定义进行解答.
解答:解:(1)如图,∵ AD⊥BC,AD=9,tan∠ABD=
AD⊥BC,AD=9,tan∠ABD=
,
∴
=
=
.
∴BD=12,
由勾股定理,得
AB=
=
=15,即AB=15.
(2)∵AD⊥BC,AC=9
,AD=9
∴cos∠CAD=
=
=
,即cos∠CAD=
.
 AD⊥BC,AD=9,tan∠ABD=
AD⊥BC,AD=9,tan∠ABD=| 3 |
| 4 |
∴
| AD |
| BD |
| 9 |
| BD |
| 3 |
| 4 |
∴BD=12,
由勾股定理,得
AB=
| AD2+BD2 |
| 92+122 |
(2)∵AD⊥BC,AC=9
| 5 |
∴cos∠CAD=
| AD |
| AC |
| 9 | ||
9
|
| ||
| 5 |
| ||
| 5 |
点评:本题考查了解直角三角形,主要利用了锐角三角函数的定义和勾股定理求得相关线段的长度.

练习册系列答案
相关题目
如图,是用火柴棒按规律拼成的图形,则第6个图形中一共有( )个平行四边形.

| A、6 | B、7 | C、8 | D、9 |
 如图,△ABC中,D、E分别是AB和AC的中点.△ABC的周长为8,则△ADE的周长是
如图,△ABC中,D、E分别是AB和AC的中点.△ABC的周长为8,则△ADE的周长是 张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图(1),然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为10cm的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x,
张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图(1),然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为10cm的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x, 如图,直线AB、CD相交于点O,OE平分∠BOD,AOD-∠DOB=72°.求∠AOC和∠DOE的度数.
如图,直线AB、CD相交于点O,OE平分∠BOD,AOD-∠DOB=72°.求∠AOC和∠DOE的度数.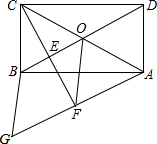 如图,在矩形ABCD中,AC、BD相交于点O,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BO,连接BG、DF.若AG=13,CF=6,求四边形BOFG的周长.
如图,在矩形ABCD中,AC、BD相交于点O,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BO,连接BG、DF.若AG=13,CF=6,求四边形BOFG的周长.